VCF: Part 3 - Diode Ladders

1 Intro

Figure 1: VCF Eurorack module (left) and VCV Model (right)

In this post we’ll be continuing to reproduce the designs of the mki x es.edu eurorack VCF. The detailed build instructions (source: https://www.ericasynths.lv/shop/diy-kits-1/edu-diy-vcf/) contain lots of great information and it’s recommended to read that document first.

This part focuses on advanced diode ladder designs. For earlier posts on basic RC designs see Part 1 and for resonant RC designs see Part 2.

2 Simplest diode ladder filter

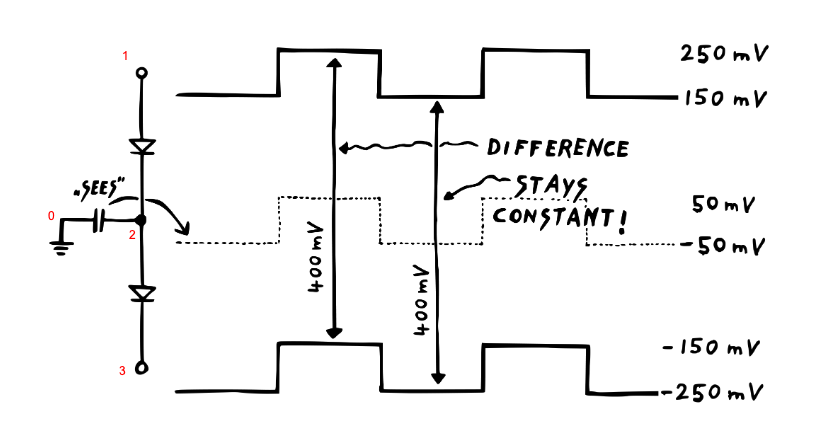
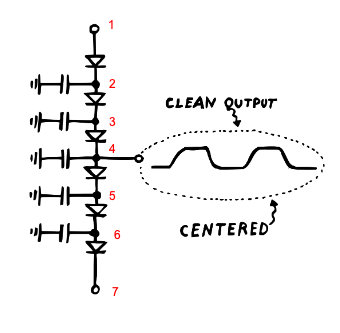
Figure 2: Simplest diode ladder filter

We can easily create copies of the input signal and shift by $\pm$ offset. As Moritz explains, this means the voltage difference ($2\times$ offset V) is constant and so the bias current going through the diodes is constant. Diodes act as voltage dependent resistors, and if the offset voltage (and therefore the voltage difference) get larger, then the effective resistance $R_{diode}$ gets smaller. Looking at Figure 2, if we replace the diodes with resistors, then it looks like a low-pass RC filter, with cutoff $f_{cutoff}\approx \frac{1}{R_{diode}C}$, and so we expect the cutoff frequency to increase as offset increases. Indeed we see this in the plots below:

def generate_diode_1_pole(V_offset, ppv=0.1, running_average_window=16):
    # output is node 2
    netlist = """
        V0 1 0 Vin_plus
        D1 1 2
        C1 2 0 1e-9        
        D2 2 3
        V1 3 0 Vin_neg
        J 2 0
    """
    class_name = "Diode1Poler" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method="LUsolve", simplify_sol=False
    )

    offset, Vin, Vin_plus, Vin_neg = symbols("offset, Vin, Vin_plus, Vin_neg")
    rules.constants.append(Assignment(Vin_plus, Vin + offset))
    rules.constants.append(Assignment(Vin_neg, Vin - offset))

    file_name = "diode_ladder"
    code_string = generate_processor(rules)

    tmax, dt = 0.1, 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    saw_fn = square(freq=50, ppv=ppv)
    v_ins = saw_fn(ts)

    with ModuleLoader(code_string, class_name) as m:
        v_outs = []
        for v_in in v_ins:
            v_out = m.process(v_in, V_offset, dt)
            v_outs.append(v_out)

        m.reset()
        # note: we must use noise of a much smaller amplitude for this to work, plus apply a little smoothing
        fs, H_dB, _, _ = calculate_filter_response(
            m,
            args=(V_offset,),
            amplitude_scale=0.05 * ppv,
            running_average_window=running_average_window,
        )

    return ts, v_ins, np.array(v_outs), fs, H_dB

2.1 Time series and frequency response

Below we plot how a square wave is filtered as a function of $V_{offset}$ (top), and how the frequency response looks (again as a function of $V_{offset}$). Note that because the diodes are nonlinear, the frequency response isn’t strictly defined. But if we use low amplitude noise then the operation is approximately linear and we can graph the response.

fig, axs = plt.subplots(2, 1, figsize=(12, 12))

for i, offset in enumerate([0.04, 0.08, 0.16, 0.32]):
    ts, v_ins, v_outs, fs, H_dB = generate_diode_1_pole(V_offset=offset, ppv=0.1)

    axs[0].plot(ts, v_ins + offset, ":", color=colors[i])
    axs[0].plot(ts, v_ins - offset, ":", label=f"V_in ± {offset:.2g}V", color=colors[i])
    axs[0].plot(ts, v_outs, label=f"V_out ({offset:.2g}V)", color=colors[i])

    axs[1].semilogx(fs, H_dB, label=f"$V_{{offset}} = {offset:.2g}V$")

axs[0].set(xlabel="t")
axs[0].legend()

num_octaves = 7
axs[1].plot(
    [2, 2 * (2**num_octaves)],
    [-10, -10 - num_octaves * 6],
    "--",
    color="k",
    label=f"6dB / oct reference",
)
axs[1].set(xlabel="frequency", ylabel="gain", ylim=(-70, 6))
axs[1].set_title("Frequency Response as function of $V_{offset}$")
axs[1].legend()
axs[1].grid()
plt.show()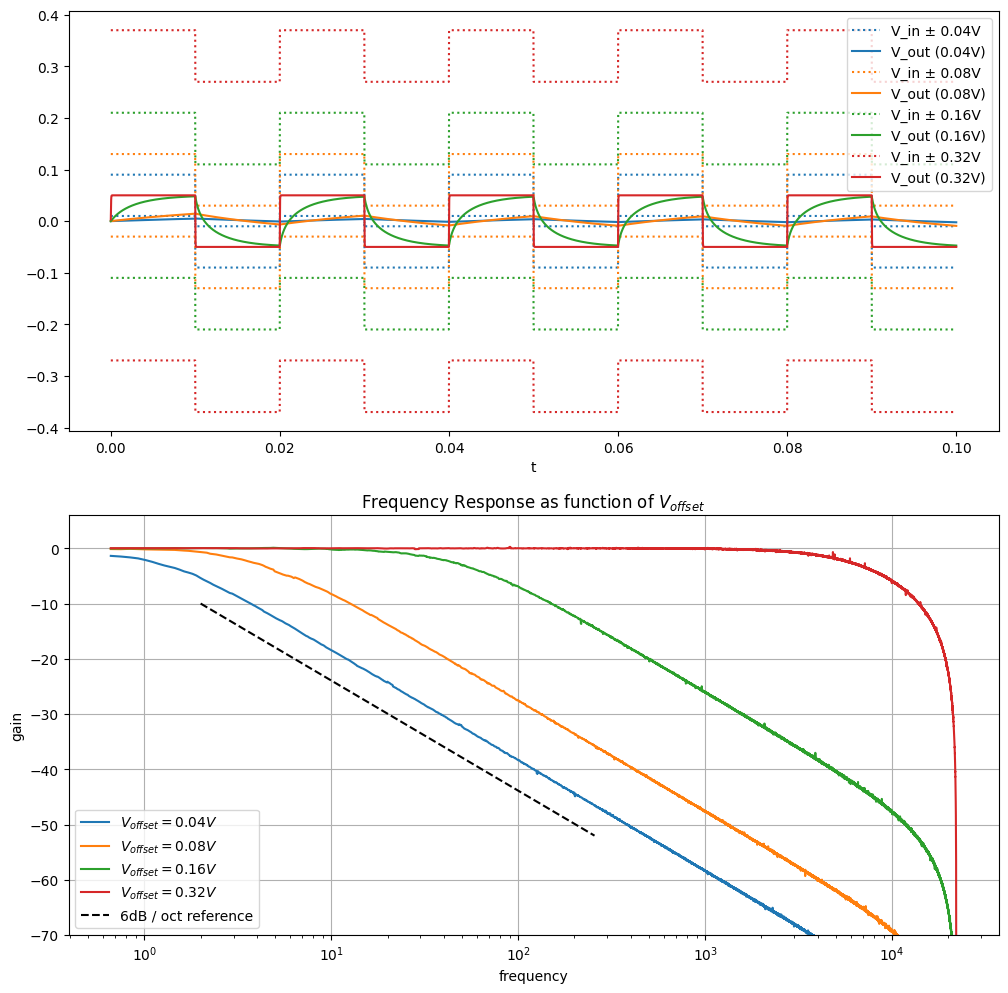

2.2 Effect of peak-to-peak voltage (ppV)

The input signal amplitude (e.g. peak-to-peak voltage (ppV)) needs to be kept very low. A small change in voltage will have a small effect on the bias current, but for larger changes in voltage, the bias current (and therefore effective resistance) will vary a lot. The top/middle plots shows that for small ppV, the response is like a typical low pass filter, but larger voltages produce an overshoot distortion.

At high input amplitudes the cutoff point is less well defined. We can simulate by scaling the noise that is used to generate frequency response plots (bottom plot).

fig, axs = plt.subplots(3, 1, figsize=(12, 12))

for ppv in [0.4, 0.2, 0.1, 0.05]:
    ts, v_ins, v_outs, fs, H_dB = generate_diode_1_pole(
        V_offset=0.3, ppv=ppv, running_average_window=None
    )
    axs[0].plot(ts, v_outs, label=f"V_outs (ppV = {ppv})")
    axs[1].plot(ts, v_outs / ppv, label=f"V_outs (ppV = {ppv})")
    axs[2].semilogx(fs, H_dB, "--", label=f"noise with stdv = {0.05*ppv:.2g}V")

axs[0].set(xlim=(0.018, 0.022), xlabel="time", ylabel="voltage")
axs[0].legend()
axs[1].set(xlim=(0.018, 0.022), xlabel="time", ylabel="normalised voltage")
axs[1].legend()
axs[2].set(
    title="Frequency reponse as a function of noise amplitude",
    xlabel="frequency",
    ylabel="gain",
    ylim=(-40, 20),
)
axs[2].legend()

plt.show()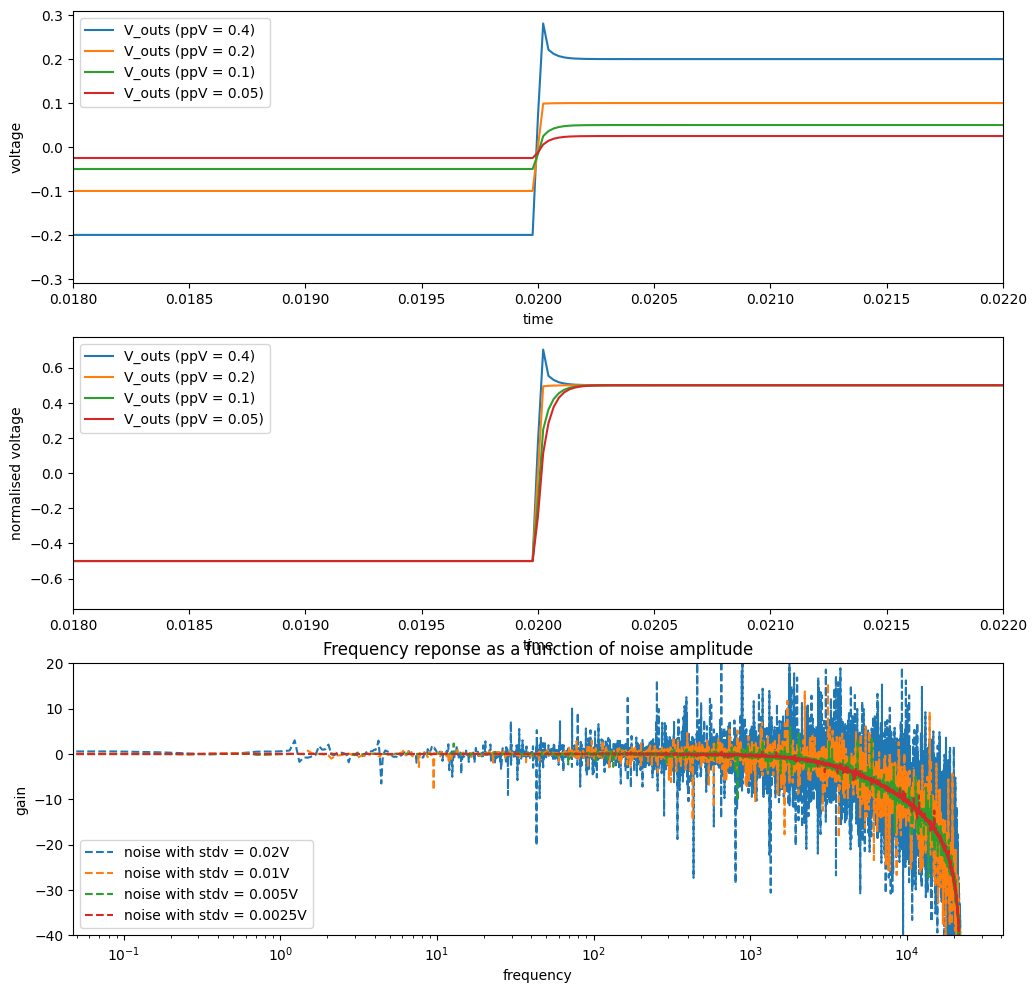

3 Multi-stage ladder

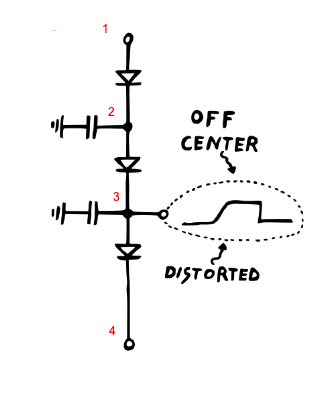
3.1 Odd vs even

Figure 3: Even number of stages

If an even number of stages are used, then there isn’t an obvious choice for which node to use as the output. As shown below, while the signal is filtered, neither output $V_2$ or $V_3$ is centered about zero. Also $V_2$ filters the downward drop in voltage more strongly whereas $V_3$ filters the rising voltage more strongly. This shows that we need to make sure the total number of stages is odd.

def generate_diode_even_stages():
    # output is node 2
    netlist = """
        V0 1 0 Vin_plus
        D1 1 2
        C1 2 0 1e-9        
        D2 2 3
        C2 3 0 1e-9
        D3 3 4
        V1 4 0 Vin_neg
        J2 2 0
        J3 3 0
    """
    class_name = "Diode1Poler" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method="LUsolve", simplify_sol=False
    )

    offset, Vin, Vin_plus, Vin_neg = symbols("offset, Vin, Vin_plus, Vin_neg")
    rules.constants.append(Assignment(Vin_plus, Vin + offset))
    rules.constants.append(Assignment(Vin_neg, Vin - offset))

    file_name = "diode_ladder"
    code_string = generate_processor(rules)

    fig, axs = plt.subplots(1, 1, figsize=(12, 5))

    tmax, dt = 0.1, 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    square_fn = square(freq=50, ppv=0.05)
    v_ins = square_fn(ts)
    offset = 0.3

    with ModuleLoader(code_string, class_name) as m:
        m.reset()
        v_outs = []

        for v_in in v_ins:
            v_out_upper, v_out_lower = m.process(v_in, offset, dt)
            v_outs.append([v_out_upper, v_out_lower])
        v_outs = np.array(v_outs)
        axs.plot(ts, v_ins, label="V_in", color=colors[0])
        axs.plot(ts, v_outs[:, 0], label="V_2", color=colors[1])
        axs.plot(ts, v_outs[:, 1], "--", label="V_3", color=colors[2])
        axs.plot(ts, 0.2 + v_outs[:, 1], "--", label="V_3 + 0.2V", color=colors[3])
        axs.set_xlabel("time")
        axs.legend()
    plt.show()


generate_diode_even_stages()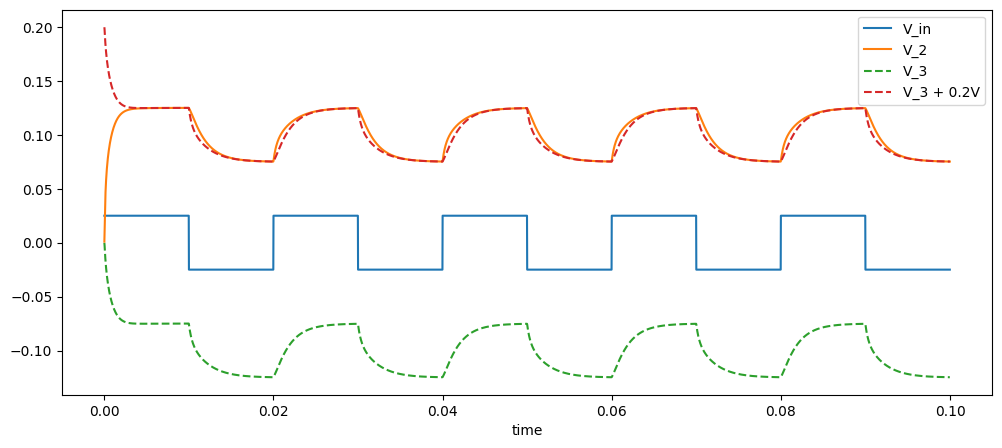

3.2 Arbitrary order multi-stage

Figure 4: Odd number of stages (third order, five stages)

Like with the RC filters, we can programmatically generate netlists for arbitrary order diode ladder filters. Figure 4 shows a three-pole (five stage) example.

def generate_diode_ladder_multi(order=3, V_offset=0.0):
    stages = 2 * order - 1

    netlist = "V0 1 0 Vin_plus\n"
    for s in range(stages):
        stage = s + 1
        netlist += f"D{stage} {stage} {stage+1}\n"
        netlist += f"C{stage} {stage+1} 0 1e-9\n"
    stage += 1
    netlist += f"D{stage} {stage} {stage+1}\n"
    netlist += f"V1 {stage+1} 0 Vin_neg\n"
    netlist += f"J {order + 1} 0"
    assumptions = {}
    class_name = "DiodeLadderMulti" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist,
        class_name,
        method="LUsolve",
        assumptions=assumptions,
        simplify_sol=False,
    )

    offset, Vin, Vin_plus, Vin_neg = symbols("offset, Vin, Vin_plus, Vin_neg")
    rules.constants.append(Assignment(Vin_plus, Vin + offset))
    rules.constants.append(Assignment(Vin_neg, Vin - offset))
    code_string = generate_processor(rules)

    tmax, dt = 0.5, 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    saw_fn = saw(freq=10, ppv=0.1)
    v_ins = saw_fn(ts)

    with ModuleLoader(code_string, class_name) as m:
        v_outs = []
        for v_in in v_ins:
            v_out = m.process(v_in, V_offset, dt)
            v_outs.append(v_out)

        m.reset()
        # note: we must use noise of a much smaller amplitude for this to work, also apply running
        # average to smooth the data a little
        fs, H_dB, _, _ = calculate_filter_response(
            m, args=(V_offset,), amplitude_scale=0.01, running_average_window=16
        )

    return ts, v_ins, v_outs, fs, H_dB, netlist


fig, axs = plt.subplots(2, 1, figsize=(12, 10))

for order in [1, 2, 3, 4]:
    # heuristic scaling of offset voltage to compensate for order
    V_offset = 0.1 * np.power(order, 1.4)

    ts, v_ins, v_outs, fs, H_dB, netlist = generate_diode_ladder_multi(
        order=order, V_offset=V_offset
    )

    axs[0].plot(ts, v_outs, label=f"order {order}")
    axs[1].semilogx(fs, H_dB, label=f"order {order}, $V_{{offset}} = {V_offset:.2g}V$")

    if order == 3:
        display(Markdown("**Example netlist: 3rd order**"))
        print(netlist)

for order in [1, 2, 3, 4]:
    num_octaves = 7
    axs[1].plot(
        [45, 45 * (2**num_octaves)],
        [-10, -10 - num_octaves * 6 * order],
        "--",
        color=colors[order - 1],
        label=f"{6*order}dB / oct reference",
    )

axs[0].plot(ts, v_ins, "--", color="k")
axs[0].legend()

axs[1].set(title="Frequency Response: nth order Diode Ladder", ylim=(-100, 10))
axs[1].legend()

plt.show()

Example netlist: 3rd order

V0 1 0 Vin_plus
D1 1 2
C1 2 0 1e-9
D2 2 3
C2 3 0 1e-9
D3 3 4
C3 4 0 1e-9
D4 4 5
C4 5 0 1e-9
D5 5 6
C5 6 0 1e-9
D6 6 7
V1 7 0 Vin_neg
J 4 0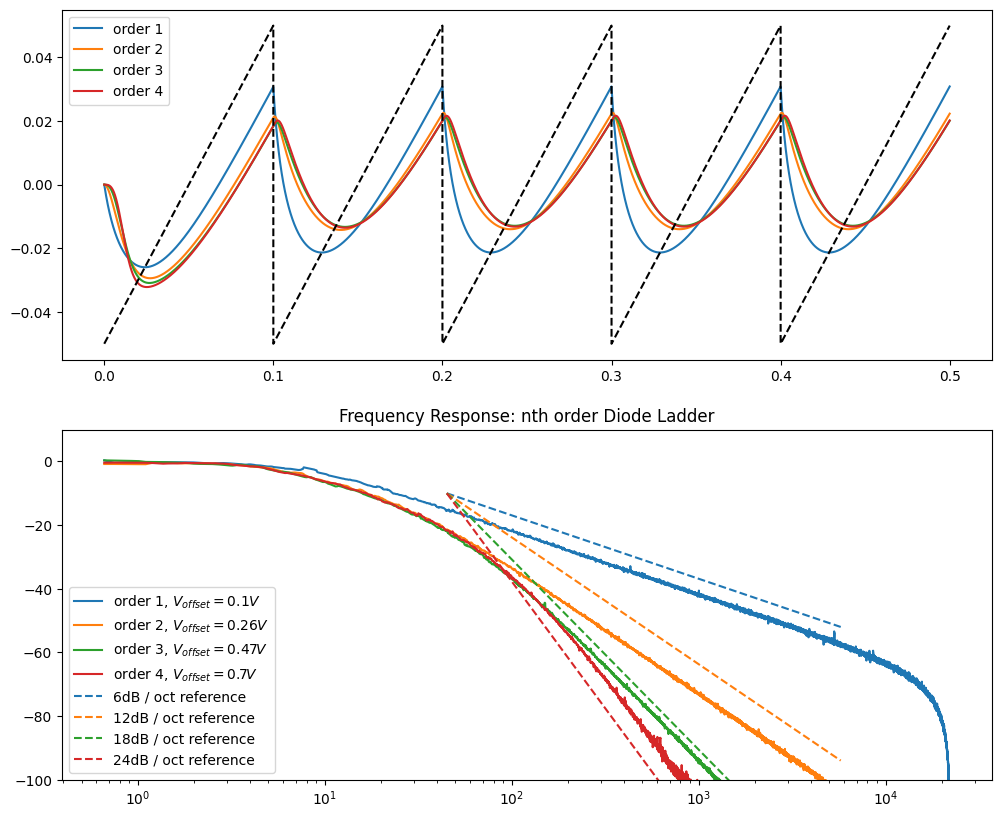

4 Driving the ladder

Figure 5: Schematic for how to pre-process voltages for the diode ladder

Because the diode ladder is sensitive to voltage levels, a preprocessing circuit is required to a) scale the voltages down in the operating range and b) offset them. There are two approaches here.

• simulate the full circuit
• arithmetically apply the same effect

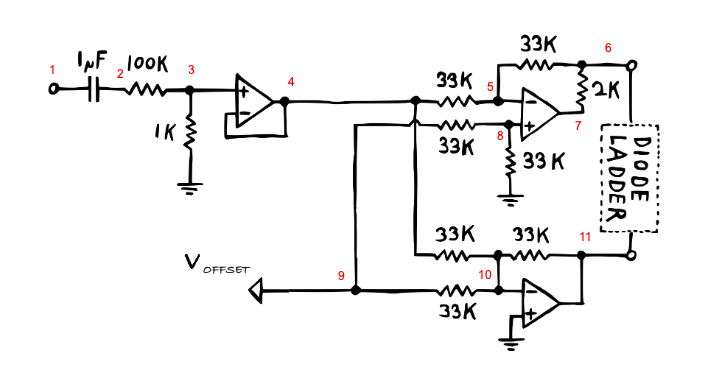
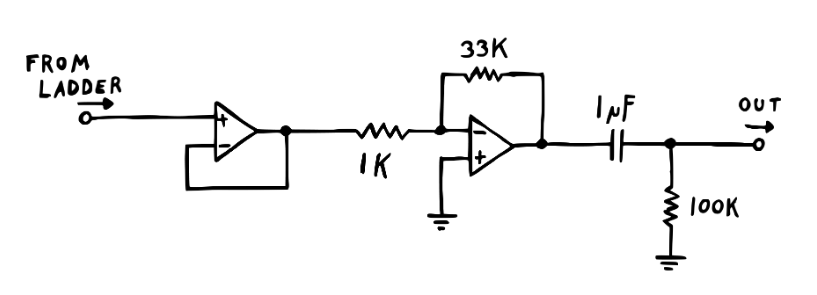
4.1 Full Circuit

The listing for the full circuit, including input and output, is shown below:

def generate_diode_ladder_multi_w_input_stage(V_offset, tmax, wave=saw):
    # mutiple stage diode ladder, with input/output circuitry
    netlist = """
        V0 1 0 Vin
        Cdc 1 2 1e-6
        R1 2 3 100000
        R1k 3 0 1000 
        Oamp 3 4 4       # buffer
        R33k 4 5 33000
        R33k 5 6 33000
        Oamp 8 5 7
        R2k 6 7 2000
        R33k 8 0 33000
        R33k 8 9 33000
        Voffset 9 0 Voffset   # simpler than pot + fixed sources
        R33k 9 10 33000
        R33k 4 10 33000
        Oamp 0 10 11
        R33k 10 11 33000      
        D1 6 12
        C1 12 0 1e-9
        D2 12 13
        C2 13 0 1e-9
        D3 13 14
        C3 14 0 1e-9
        D4 14 15
        C4 15 0 1e-9
        D5 15 16
        C5 16 0 1e-9
        D6 16 11
        Oamp 14 17 17 
        R1k 17 18 1000
        Oamp 0 18 19 
        R33k 18 19 33000       
        J 19 0
        Jpos 6 0 
        Jneg 11 0 
    """

    class_name = "DiodeLadderMultiWithIO" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method="LUsolve", simplify_sol=False
    )

    file_name = "diode_ladder_multi_w_io"
    code_string = generate_processor(rules)

    dt = 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    wave_fn = wave(freq=100, ppv=10)
    v_ins = wave_fn(ts)

    with ModuleLoader(code_string, class_name) as m:
        v_outs, v_tops, v_bots = [], [], []
        for v_in in v_ins:
            v_out, v_top, v_bot = m.process(v_in, V_offset, dt)
            v_outs.append(v_out)
            v_tops.append(v_top)
            v_bots.append(v_bot)

    return ts, v_ins, np.array(v_outs), np.array(v_tops), np.array(v_bots)

4.2 Arithmetic

Let’s instead just simulate the input section (removing the AC coupling capacitor for simplicity). As we can see the resulting voltages are very simple!

def generate_diode_ladder_input_stage_only():
    # mutiple stage diode ladder, with input/output circuitry
    netlist = """
        V0 1 0 V_in
        R1 1 2  50000  # replace cap with 2x50k (just to avoid reshuffling ids!)
        R1 2 3  50000
        R_1k 3 0 1000 
        Oamp 3 4 4       # buffer
        R33k 4 5 33000
        R33k 5 6 33000
        Oamp 8 5 7
        R2k 6 7 2000
        R33k 8 0 33000
        R33k 8 9 33000
        Voffset 9 0 V_offset   # simpler than pot + fixed sources
        R33k 9 10 33000
        R33k 4 10 33000
        Oamp 0 10 11
        R33k 10 11 33000
        Jpos 6 0
        Jneg 11 0
    """

    class_name = "DiodeLadderInput" + str(np.random.randint(100000))
    Vin, R1, R1k = symbols("V_in, R1, R_1k", positive=True)
    rules, (A, x, b) = run_MNA(
        netlist,
        class_name,
        method="LUsolve",
        simplify_sol=False,
        assumptions={R1: 50 * R1k},
    )

    show_sol = lambda i: display(
        Eq(rules.solutions[i].lhs, simplify(rules.solutions[i].rhs))
    )
    show_sol(6)
    show_sol(11)


generate_diode_ladder_input_stage_only()

${\displaystyle v_6=\frac{2R_1{V}_{offset}-R_{1k}{V}_{in}+R_{1k}{V}_{offset}}{2R_1+R_{1k}}}$

${\displaystyle v_{11}=\frac{-2R_1{V}_{offset}-R_{1k}{V}_{in}-R_{1k}{V}_{offset}}{2R_1+R_{1k}}}$

Figure 6: Diode ladder output stage

This means we can just simulate the ladder itself, given we pre-scale the voltages. We can do the same analysis with the output stage, which yields $V_{out}=-33V_{ladder}$.

def generate_diode_ladder_multi(V_scale, V_offset, tmax, wave=saw):
    # output is node 4
    netlist = """
        V0 1 0 Vin_plus
        D1 1 2
        C1 2 0 1e-9
        D2 2 3
        C2 3 0 1e-9
        D3 3 4
        C3 4 0 1e-9
        D4 4 5
        C4 5 0 1e-9
        D5 5 6
        C5 6 0 1e-9
        D6 6 7
        V1 7 0 Vin_neg
        J 4 0
    """

    class_name = "DiodeLadderMulti" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method="LUsolve", simplify_sol=False
    )

    offset, Vin, scale, Vin_plus, Vin_neg = symbols(
        "offset, Vin, scale, Vin_plus, Vin_neg"
    )
    rules.constants.append(Assignment(Vin_plus, scale * Vin + offset))
    rules.constants.append(Assignment(Vin_neg, scale * Vin - offset))

    file_name = "diode_ladder_multi"
    code_string = generate_processor(rules)

    dt = 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    wave_fn = wave(freq=100, ppv=10)
    v_ins = wave_fn(ts)

    with ModuleLoader(code_string, class_name) as m:
        v_outs = []
        for v_in in v_ins:
            v_out = m.process(v_in, V_offset, V_scale, dt)
            v_outs.append(v_out)

    return ts, v_ins, np.array(v_outs)

for wave in [saw, square]:
    tmax, V_offset = 0.1, 0.74
    display(Markdown(f"## Waveform: {wave.__name__}"))

    fig, axs = plt.subplots(2, 1, figsize=(10, 10))
    plt.suptitle(wave.__name__)
    ts, v_ins, v_outs, v_tops, v_bots = generate_diode_ladder_multi_w_input_stage(
        V_offset=V_offset, tmax=tmax, wave=wave
    )
    axs[0].plot(ts, v_ins, "--", color="k", label="V_in")
    axs[0].plot(ts, v_tops, label=f"v_6 (top of ladder)")
    axs[0].plot(ts, v_bots, label=f"v_11 (bottom of ladder)")
    axs[0].plot(ts, v_outs, label=f"V_out")
    axs[0].legend()
    axs[0].set(xlim=[tmax - 0.05, tmax], ylim=[-6, +6], xlabel="time")

    axs[1].plot(ts, v_outs, label=f"V_out (full circuit)")

    ts, v_ins, v_ladder = generate_diode_ladder_multi(
        V_scale=-1 / 101, V_offset=V_offset, tmax=tmax, wave=wave
    )
    axs[1].plot(ts, v_ladder * -33, "--", label=f"33 × V_ladder (arithmetic)")
    axs[1].set_xlabel("time")
    axs[1].legend()
    plt.tight_layout()
    plt.show()

4.3 Waveform: saw

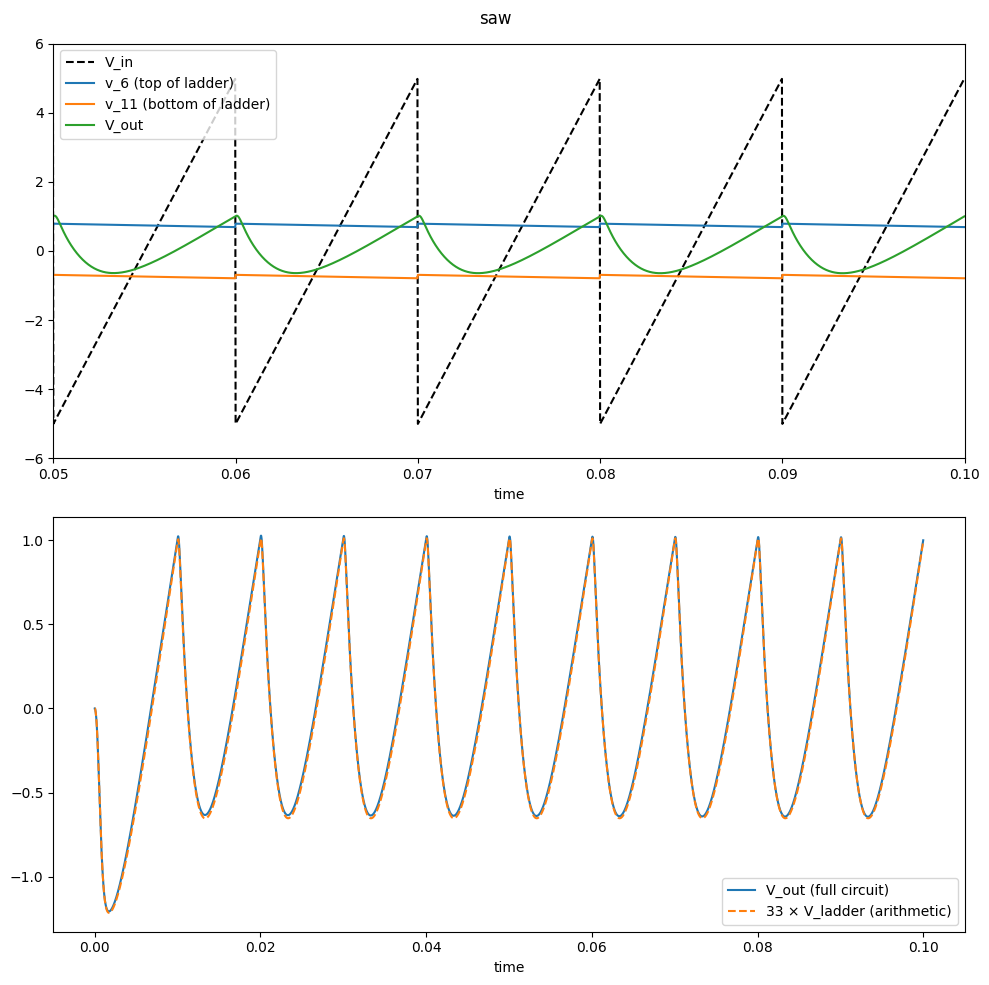
4.4 Waveform: square

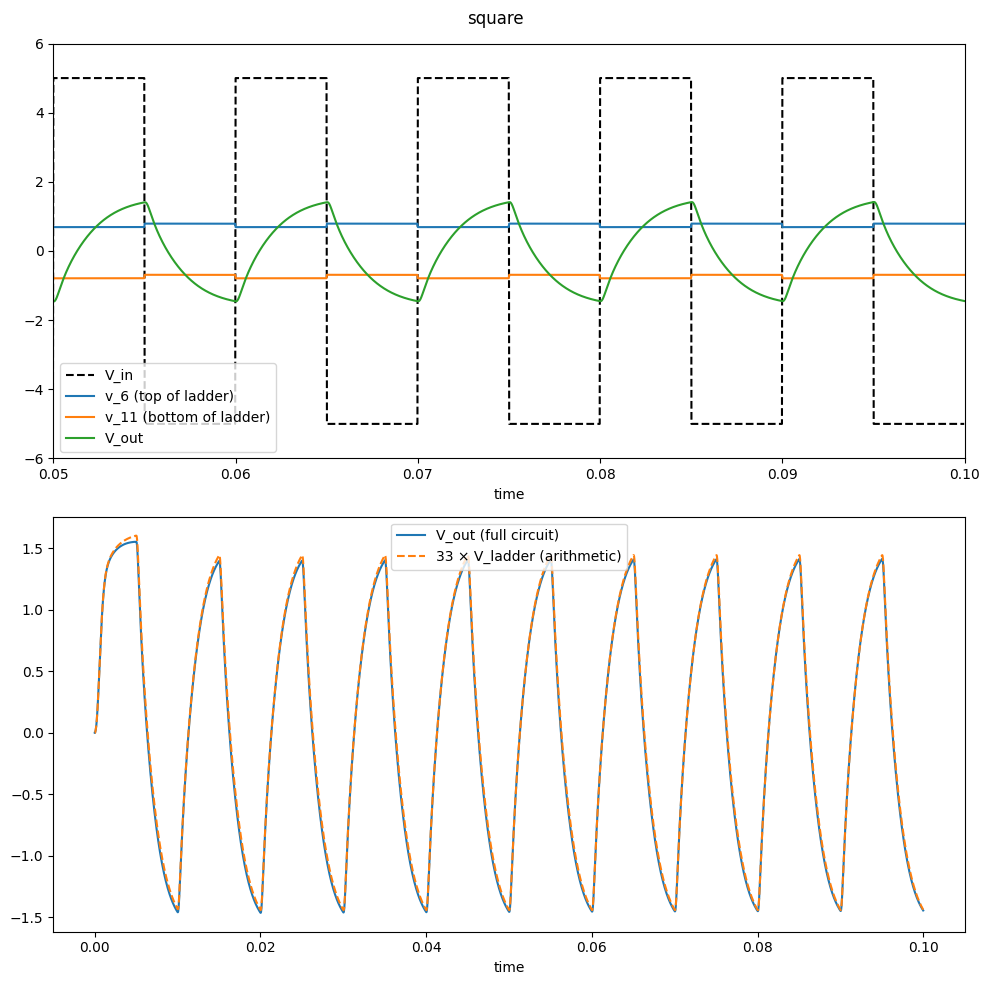
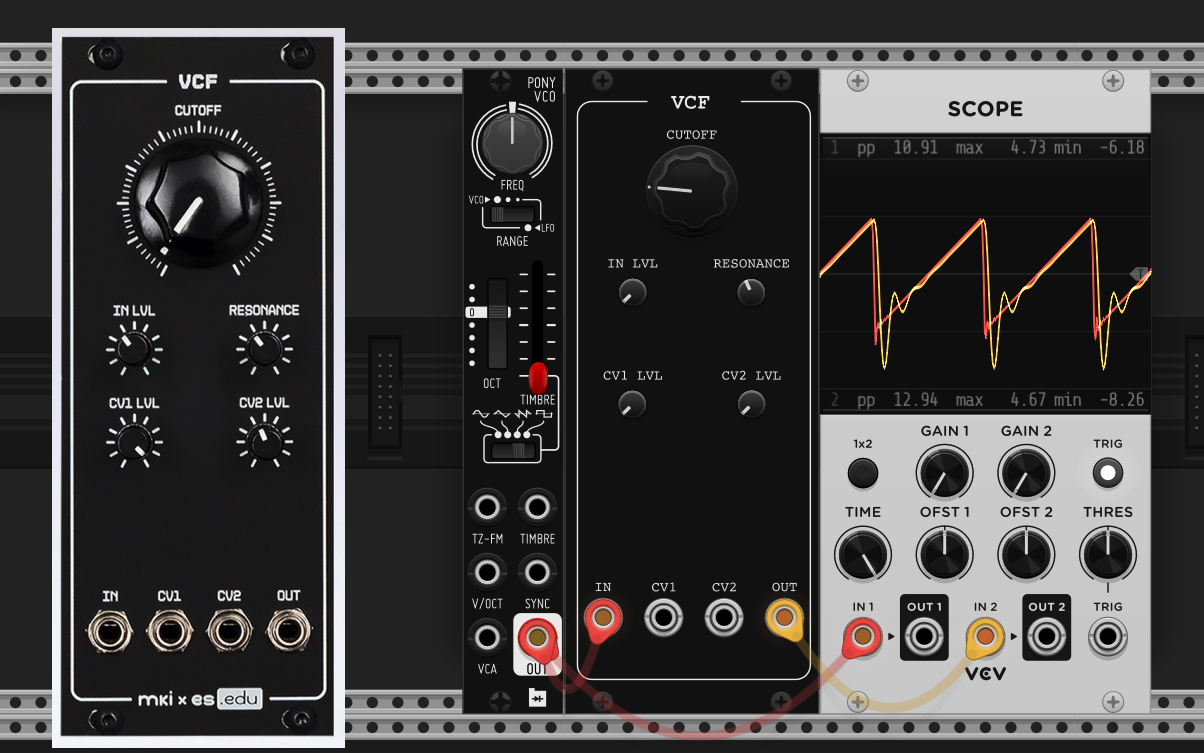
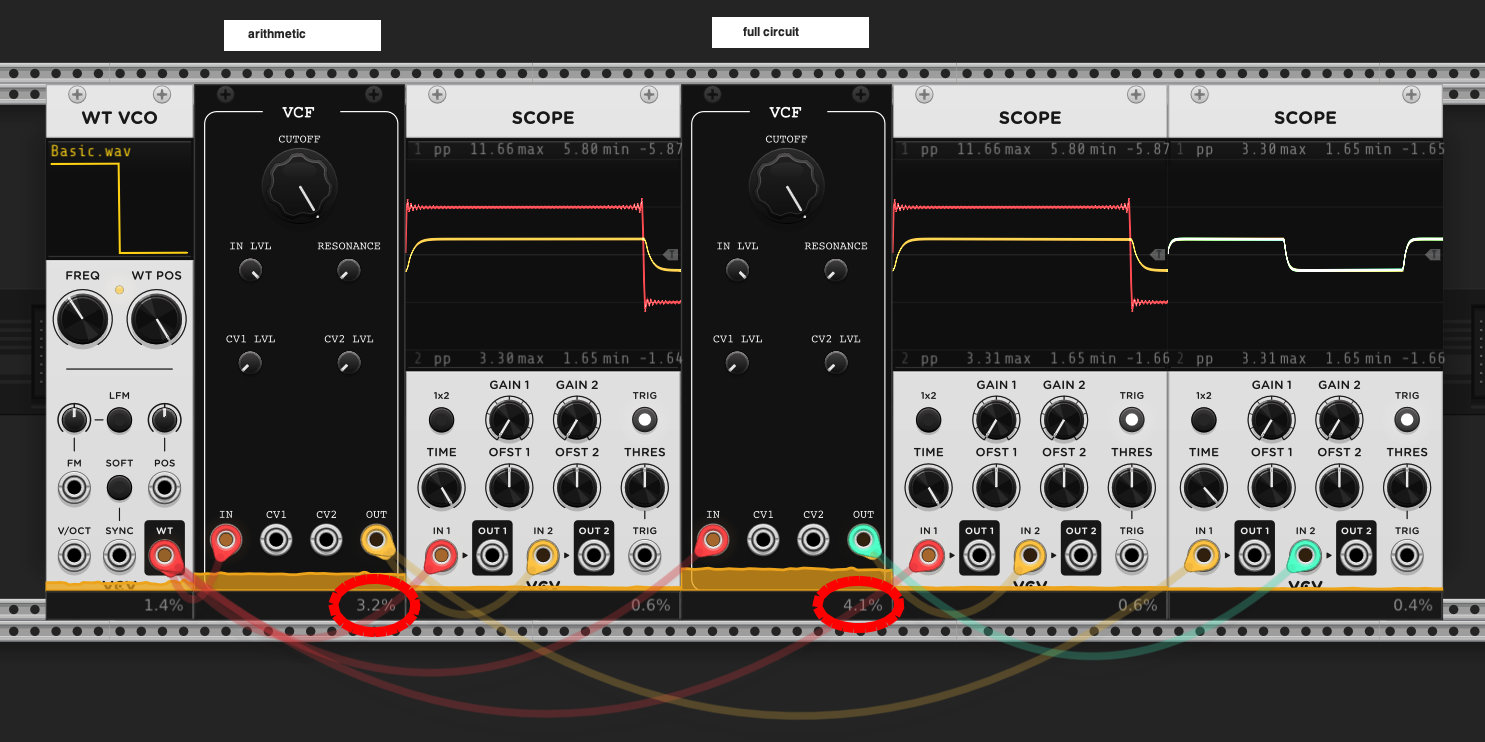
4.5 CPU Comparison

Figure 7: CPU usage is reduced for the arithmetic approach

Finally having ported these engines to VCV Rack, we can see that the waveforms are the same, but the arithmetic uses 25% less CPU.

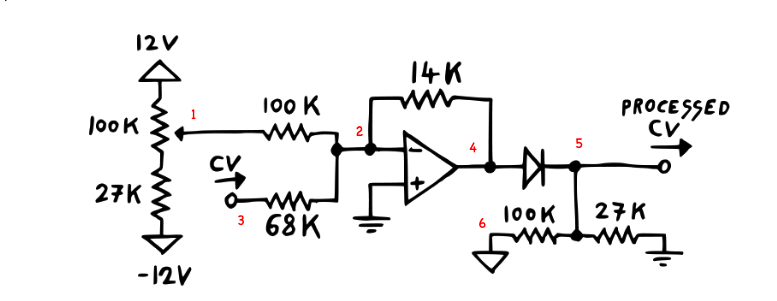
5 CV processing

Figure 8: CV processing schematic

def generate_diode_ladder_cv_stage_only():
    # https://tinyurl.com/2nn6clc9
    netlist = """
        Voffset 1 0 V_offset   # simpler than pot + fixed sources
        R_1 1 2  100000
        Vcv 3 0 V_cv        
        R_68k 3 2 68000
        Oamp 0 2 4
        R_14k 2 4 14000
        D1 4 5
        R_100k 6 5 100000
        R_27k 5 0 27000
        Vcc 6 0 -12.  
        J 5 0
    """

    class_name = "DiodeLadderInput" + str(np.random.randint(100000))
    Vin, R1, R1k = symbols("V_in, R1, R_1k")
    rules, (A, x, b) = run_MNA(
        netlist,
        class_name,
        method="LUsolve",
        simplify_sol=True,
        assumptions={R1: 50 * R1k},
    )

    show_sol = lambda i: display(
        Eq(rules.solutions[i].lhs, simplify(rules.solutions[i].rhs))
    )
    show_sol(5)

    file_name = "diode_ladder_input"
    code_string = generate_processor(rules)

    dt = 1.0 / 44100.0
    v_cvs = np.linspace(-10, +10, 11)
    v_offsets = np.arange(+12, -6, -0.5)
    with ModuleLoader(code_string, class_name) as m:
        fig, ax = plt.subplots(figsize=(12, 5))

        for v_cv in v_cvs:
            v_outs = []
            for v_offset in v_offsets:
                v_out = m.process(v_cv, v_offset, dt)
                v_outs.append(v_out)

                if np.allclose(v_offset, 0.0) and np.allclose(v_cv, 0.0):
                    print(f"v_cv = v_offset = 0, v_out = {v_out}")

            if v_cv == 0:
                ax.plot(v_offsets, v_outs, "--", label=f"V_cv = {v_cv}", color="k")
            else:
                ax.plot(v_offsets, v_outs, label=f"V_cv = {v_cv}")
        ax.legend()
        ax.grid()
        ax.set(xlabel="V_offset")
        plt.show()

    return ts, v_ins, np.array(v_outs)


_ = generate_diode_ladder_cv_stage_only()

${\displaystyle v_5=\frac{R_{27k}(-R_1{R}_{100k}{R}_{14k}{V}_{cv}d1.geq+R_1{R}_{100k}{R}_{68k}d1.ieq+R_1{R}_{68k}Vcc-R_{100k}{R}_{14k}{R}_{68k}{V}_{offset}d1.geq)}{R_1{R}_{68k}(R_{100k}{R}_{27k}d1.geq+R_{100k}+R_{27k})}}$

v_cv = v_offset = 0, v_out = -0.4784405529499054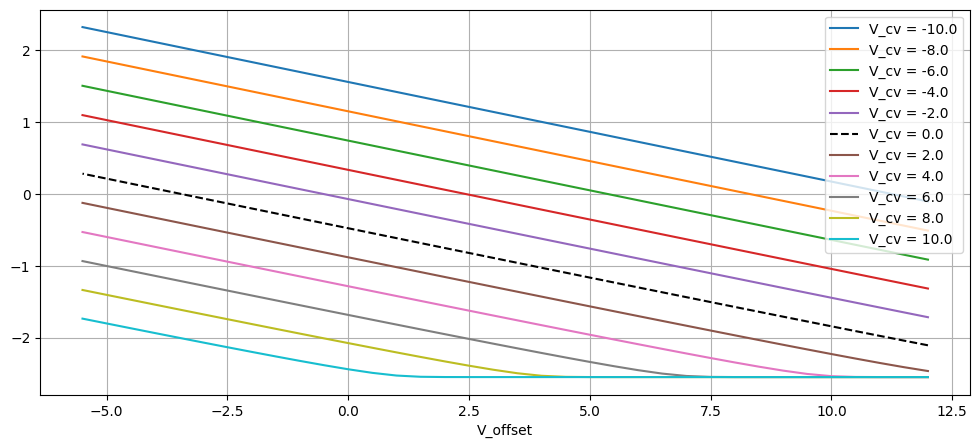

6 Resonance II

Figure 9: Resonance schematic

def generate_diode_ladder_multi_resonance(V_scale, V_offset, tmax, yr, wave=saw):
    # https://tinyurl.com/2z2lbzy3
    netlist = """
        V0 1 0 Vin_plus
        D1 1 2
        C1 2 11 1e-9
        D2 2 3
        C2 3 0 1e-9
        D3 3 4
        C3 4 0 1e-9
        D4 4 5
        C4 5 0 1e-9
        D5 5 6
        C5 6 11 1e-9
        D6 6 7
        V1 7 0 Vin_neg  
        Oamp 4 8 8
        Pr 0 9 8 100000
        Oamp 9 10 11        
        R100k 10 11 100000
        Dp1 10 11 
        Dp2 11 10 
        Rtrim 10 0 20000           # effectively trimmer
        J 8 0
    """

    class_name = "DiodeLadderMultiResonance" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method="LUsolve", simplify_sol=False
    )

    offset, Vin, scale, Vin_plus, Vin_neg = symbols(
        "offset, Vin, scale, Vin_plus, Vin_neg"
    )
    rules.constants.append(Assignment(Vin_plus, scale * Vin + offset))
    rules.constants.append(Assignment(Vin_neg, scale * Vin - offset))

    file_name = "diode_ladder_multi_resonance"
    code_string = generate_processor(rules)
    print(yr)
    # print(code_string)

    dt = 0.5 / 44100.0
    ts = np.arange(0, tmax, dt)
    wave_fn = wave(freq=100, ppv=10)
    v_ins = wave_fn(ts)

    with ModuleLoader(code_string, class_name) as m:
        v_outs = []
        for v_in in v_ins:
            v_out = m.process(v_in, V_offset, V_scale, yr, dt)
            v_outs.append(v_out)

    return ts, v_ins, np.array(v_outs)


V_offset = 0.9
fig, ax = plt.subplots(figsize=(12, 5))

for yr in [0.25, 0.5, 0.75]:
    ts, v_ins, v_outs = generate_diode_ladder_multi_resonance(
        V_scale=1 / 101, V_offset=V_offset, tmax=0.025, yr=yr, wave=square
    )
    if yr == 0.25:
        ax.plot(ts, v_ins, "--", color="k")
    ax.plot(ts, 33 * v_outs, label=f"y_r = {yr}")

ax.legend()
plt.show()

0.25
0.5
0.75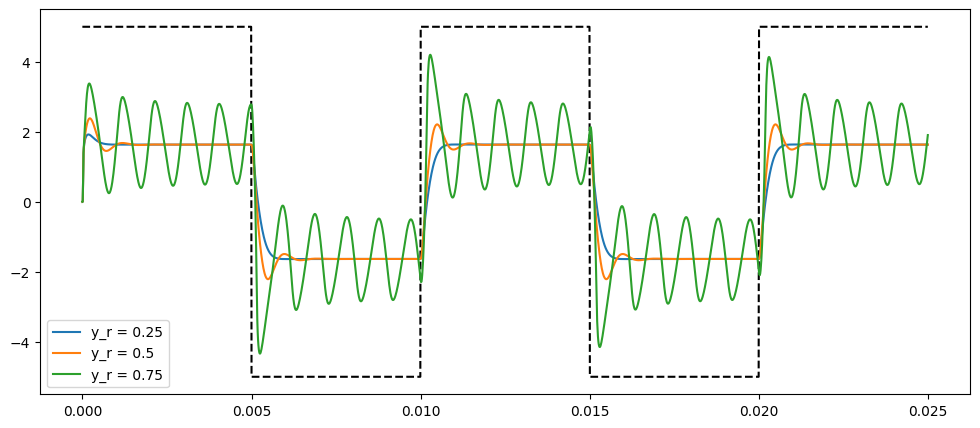

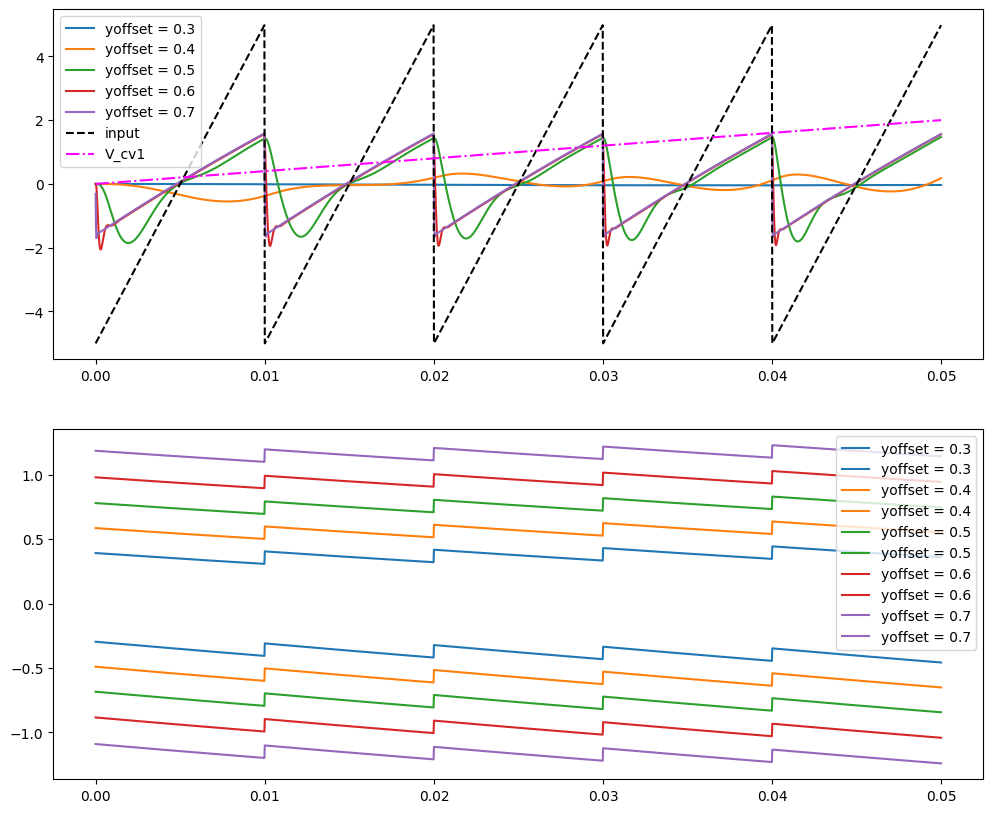
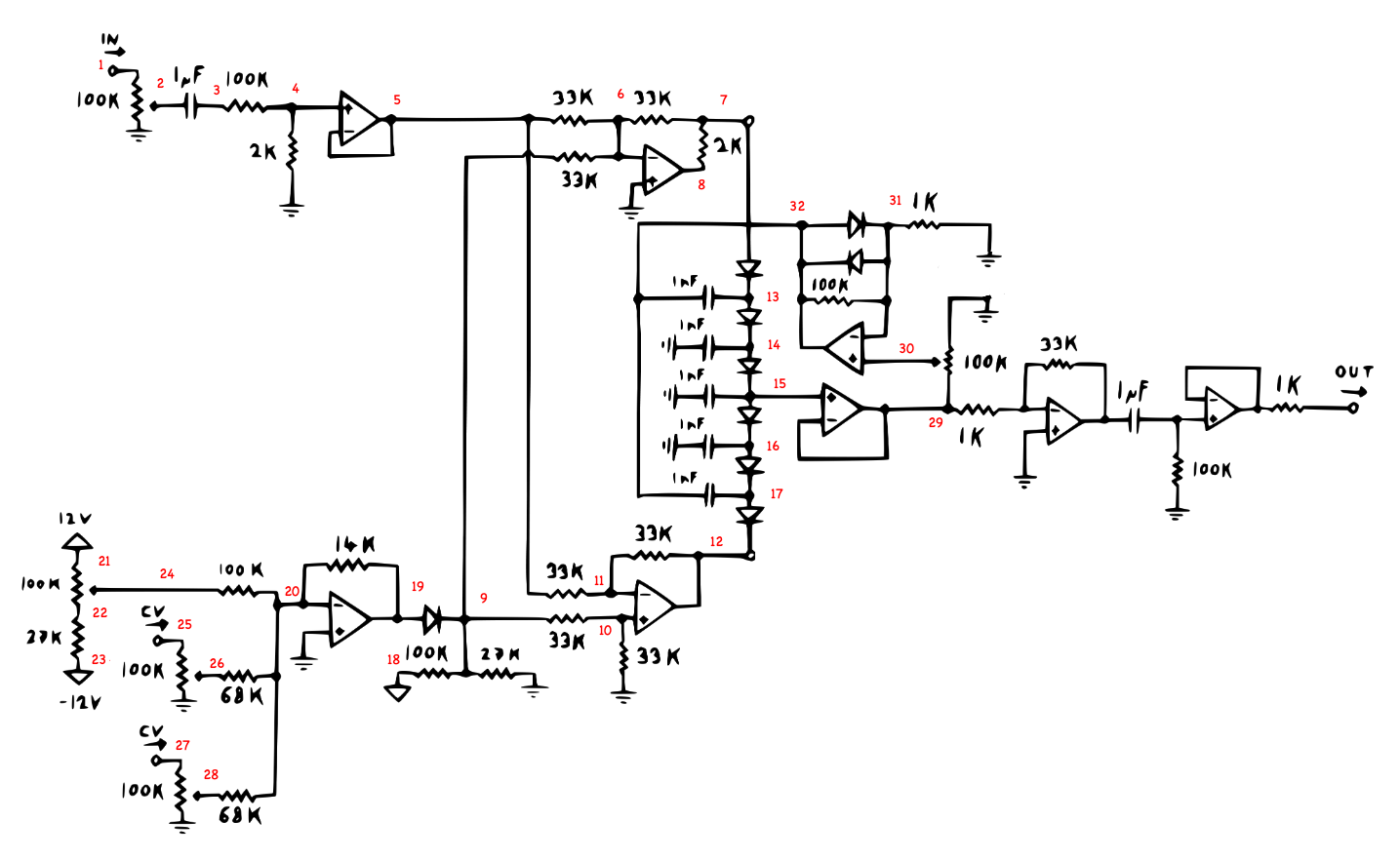
7 Final Circuit

Figure 10: Full schematic

def generate_diode_ladder_full_no_res(ygain, tmax, ycv1=0.99, ycv2=0.99, wave=saw):
    # mutiple stage diode ladder, with input/output circuitry
    netlist = """
        # input and DC coupling
        V0 1 0 Vin
        Pgain 0 2 1 100000
        Cdc 2 3 1e-6
        R1 3 4 100000
        R1k 4 0 1000 
        Oamp 4 5 5       # buffer
        
        R33k 5 6 33000
        R33k 6 7 33000
        R2k 7 8 2000
        Oamp 0 6 8
        R33k 9 6 33000        
        R33k 9 10 33000
        R33k 10 0 33000
        Oamp 10 11 12
        R33k 5 11 33000
        R33k 11 12 33000      
                
        # 7 top of ladder, 12 bottom
        D1 7 13
        C1 13 0 1e-9
        D2 13 14
        C2 14 0 1e-9
        D3 14 15
        C3 15 0 1e-9
        D4 15 16
        C4 16 0 1e-9
        D5 16 17
        C5 17 0 1e-9
        D6 17 12    

        # cutoff and cv section
        Vneg1 18 0 -12.0
        R100k 18 9 100000
        R27k 9 0 27000
        Dcv 19 9             
        Oamp 0 20 19 
        R14k 19 20 14000
        Vpos 21 0 +12.0
        Vneg 23 0 -12.0
        Poffset 22 24 21 100000
        R27k 22 23 27000
        R100k 20 24 100000        
        # cv inputs
        Vcv1 25 0 Vin_cv1
        Pcv1 0 26 25 100000
        R68k 26 20 68000
        Vcv2 27 0 Vin_cv2
        Pcv2 0 28 27 100000
        R68k 28 20 68000
        J 15 0
        Jin 2 0        
    """

    R1k, R2k, R14k, R27k, R33k, R68k, R100k = symbols(
        "R1k, R2k, R14k, R27k, R33k, R68k, R100k"
    )
    Rpgain, Rpcv1, Rpcv2, Rpoffset, Rpr = symbols("Rpgain, Rpcv1, Rpcv2, Rpoffset, Rpr")
    assumptions = {
        R14k: 14 * R1k,
        R2k: 2 * R1k,
        R27k: 27 * R1k,
        R33k: 33 * R1k,
        R68k: 68 * R1k,
        R100k: 100 * R1k,
        Rpgain: 100 * R1k,
        Rpcv1: 100 * R1k,
        Rpcv2: 100 * R1k,
        Rpoffset: 100 * R1k,
        Rpr: 100 * R1k,
    }

    class_name = "DiodeLadderFull" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist,
        class_name,
        method="LUsolve",
        simplify_sol=False,
        assumptions=assumptions,
    )

    file_name = "diode_ladder_full"
    code_string = generate_processor(rules)

    for item in code_string.split("\n"):
        if "process" in item:
            print(item.strip())

    dt = 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    wave_fn = wave(freq=100, ppv=10)
    v_ins = wave_fn(ts)
    v_cv1, v_cv2 = 0.0, 0.0
    v_cv1s = np.linspace(0, 2, len(v_ins))

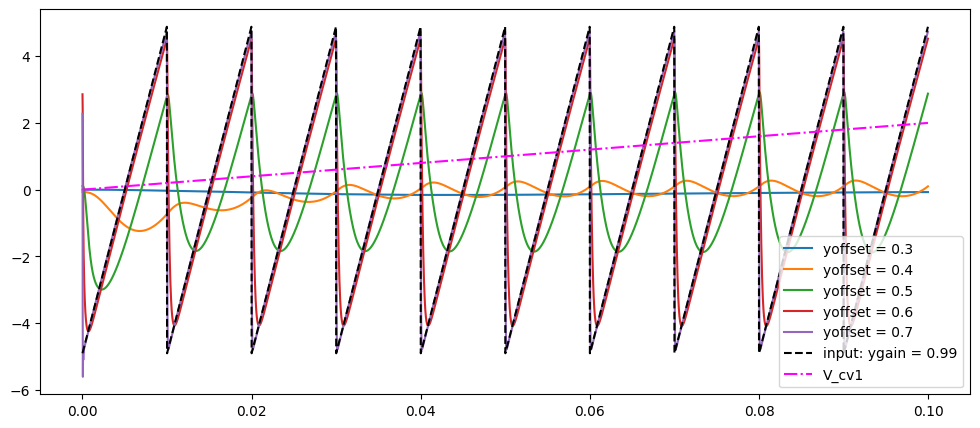
    with ModuleLoader(code_string, class_name) as m:
        fig, axs = plt.subplots(1, 1, figsize=(12, 5))

        for yoffset in [0.3, 0.4, 0.5, 0.6, 0.7]:
            v_outs = []
            for v_in, v_cv1 in zip(v_ins, v_cv1s):
                outs = m.process(v_in, v_cv1, v_cv2, ycv1, ycv2, ygain, yoffset, dt)
                v_outs.append(outs)
            v_outs = np.array(v_outs)

            axs.plot(ts, -100 * v_outs[:, 0], label=f"yoffset = {yoffset}")

        axs.plot(ts, v_outs[:, 1], "--", color="k", label=f"input: ygain = {ygain}")
        axs.plot(ts, v_cv1s, "-.", color="magenta", label=f"V_cv1")
        axs.legend()
        plt.show()


generate_diode_ladder_full_no_res(ygain=0.99, tmax=0.1, ycv1=0.99)
generate_diode_ladder_full_no_res(ygain=0.99, tmax=0.1, ycv1=0.01)

auto process(float Vin, float Vin_cv1, float Vin_cv2, float ycv1, float ycv2, float ygain, float yoffset, float T) {
auto process(float Vin, float Vin_cv1, float Vin_cv2, float ycv1, float ycv2, float ygain, float yoffset, float T) {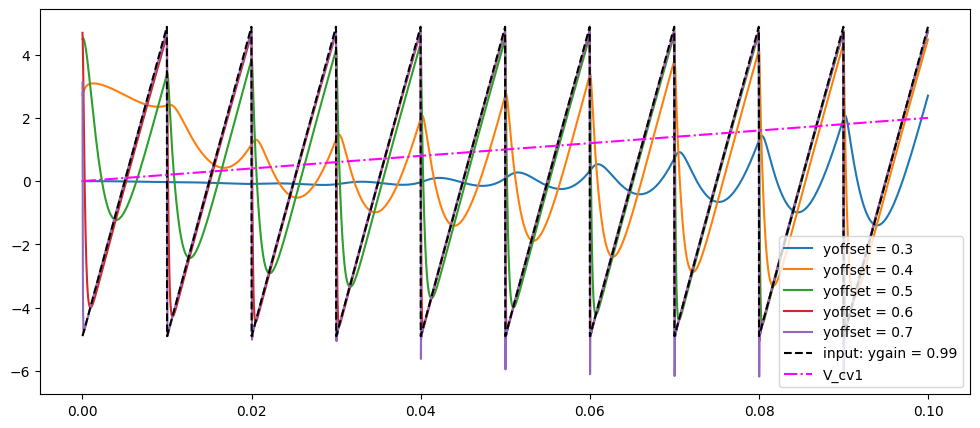

def code_diode_ladder_full_input_section():
    # mutiple stage diode ladder, with input/output circuitry
    netlist = """
        # input and DC coupling
        V0 1 0 Vin
        Pgain 0 2 1 100000
        Cdc 2 3 1e-6
        R1 3 4 100000
        R1k 4 0 1000 
        Oamp 4 5 5       # buffer
        
        R33k 5 6 33000
        R33k 6 7 33000
        R2k 7 8 2000
        Oamp 0 6 8
        R33k 9 6 33000        
        R33k 9 10 33000
        R33k 10 0 33000
        Oamp 10 11 12
        R33k 5 11 33000
        R33k 11 12 33000
        
        # cutoff and cv section
        Vneg1 13 0 -12.0
        R100k 13 9 100000
        R27k 9 0 27000
        Dcv 14 9             
        Oamp 0 15 14 
        R14k 14 15 14000
        Vpos 16 0 +12.0
        Vneg 18 0 -12.0
        
        Poffset 17 19 16 100000
        R27k 17 18 27000
        R100k 15 19 100000        
        # cv inputs
        Vcv1 20 0 Vin_cv1
        Pcv1 0 21 20 100000
        R68k 21 15 68000
        Vcv2 22 0 Vin_cv2
        Pcv2 0 23 22 100000
        R68k 23 15 68000

        # 7 top of ladder, 12 bottom
        Jpos 7 0
        Jneg 12 0
    """

    R1k, R2k, R14k, R27k, R33k, R68k, R100k = symbols(
        "R1k, R2k, R14k, R27k, R33k, R68k, R100k"
    )
    Rpgain, Rpcv1, Rpcv2, Rpoffset, Rpr = symbols("Rpgain, Rpcv1, Rpcv2, Rpoffset, Rpr")
    assumptions = {
        R14k: 14 * R1k,
        R2k: 2 * R1k,
        R27k: 27 * R1k,
        R33k: 33 * R1k,
        R68k: 68 * R1k,
        R100k: 100 * R1k,
        Rpgain: 100 * R1k,
        Rpcv1: 100 * R1k,
        Rpcv2: 100 * R1k,
        Rpoffset: 100 * R1k,
        Rpr: 100 * R1k,
    }

    class_name = "DiodeLadderFull" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist,
        class_name,
        method="LUsolve",
        simplify_sol=False,
        assumptions=assumptions,
    )

    file_name = "diode_ladder_full"
    code_string = generate_processor(rules)

    for item in code_string.split("\n"):
        if "process" in item:
            print(item.strip())

    return class_name, code_string


def code_diode_ladder_full_output_section():
    # https://tinyurl.com/2z2lbzy3
    netlist = """
        V0 1 0 Vin_plus
        D1 1 2
        C1 2 11 1e-9
        D2 2 3
        C2 3 0 1e-9
        D3 3 4
        C3 4 0 1e-9
        D4 4 5
        C4 5 0 1e-9
        D5 5 6
        C5 6 11 1e-9
        D6 6 7
        V1 7 0 Vin_neg  
        Oamp 4 8 8
        Pr 0 9 8 100000
        Oamp 9 10 11        
        R100k 10 11 100000
        Dp1 10 11 
        Dp2 11 10 
        Rtrim 10 0 20000           # effectively trimmer
        J 8 0
    """

    class_name = "DiodeLadderMultiResonance" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method="LUsolve", simplify_sol=False
    )

    # offset, Vin, scale, Vin_plus, Vin_neg = symbols("offset, Vin, scale, Vin_plus, Vin_neg")
    # rules.constants.append(Assignment(Vin_plus, scale*Vin + offset))
    # rules.constants.append(Assignment(Vin_neg, scale*Vin - offset))

    file_name = "diode_ladder_multi_resonance"
    code_string = generate_processor(rules)

    for item in code_string.split("\n"):
        if "process" in item:
            print(item.strip())

    return class_name, code_string


class_name_input, code_res_input = code_diode_ladder_full_input_section()
class_name_output, code_res_output = code_diode_ladder_full_output_section()


def generate_diode_ladder_full_concat(
    ygain, tmax, ycv1=0.99, ycv2=0.99, yr=0.5, wave=saw
):
    dt = 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    wave_fn = wave(freq=100, ppv=10)
    v_ins = wave_fn(ts)
    v_cv1, v_cv2 = 0.0, 0.0
    v_cv1s = 0 * np.linspace(0, 2, len(v_ins))

    with ModuleLoader(code_res_input, class_name_input) as m_in, ModuleLoader(
        code_res_output, class_name_output
    ) as m_out:
        fig, axs = plt.subplots(2, 1, figsize=(12, 10))

        for i, yoffset in enumerate([0.3, 0.4, 0.5, 0.6, 0.7]):
            v_ladder_inputs, v_outs = [], []
            for v_in, v_cv1 in zip(v_ins, v_cv1s):
                v_pos, v_neg = m_in.process(
                    v_in, v_cv1, v_cv2, ycv1, ycv2, ygain, yoffset, dt
                )
                outs = m_out.process(v_neg, v_pos, yr, dt)
                v_outs.append(outs)
                v_ladder_inputs.append((v_pos, v_neg))
            v_outs = np.array(v_outs)
            v_ladder_inputs = np.array(v_ladder_inputs)

            axs[0].plot(
                ts, v_ladder_inputs[:, 0], label=f"yoffset = {yoffset}", color=colors[i]
            )
            axs[0].plot(ts, v_ladder_inputs[:, 1], label=f"yoffset = {yoffset}")
            axs[1].plot(ts, 33 * v_outs, label=f"yoffset = {yoffset}")

        axs[1].plot(ts, v_cv1s, "-.", color="magenta", label=f"V_cv1")
        axs[0].legend()
        axs[1].legend()
        plt.show()


generate_diode_ladder_full_concat(ygain=0.99, tmax=0.1, ycv1=0.99)

auto process(float Vin, float Vin_cv1, float Vin_cv2, float ycv1, float ycv2, float ygain, float yoffset, float T) {
auto process(float Vin_neg, float Vin_plus, float yr, float T) {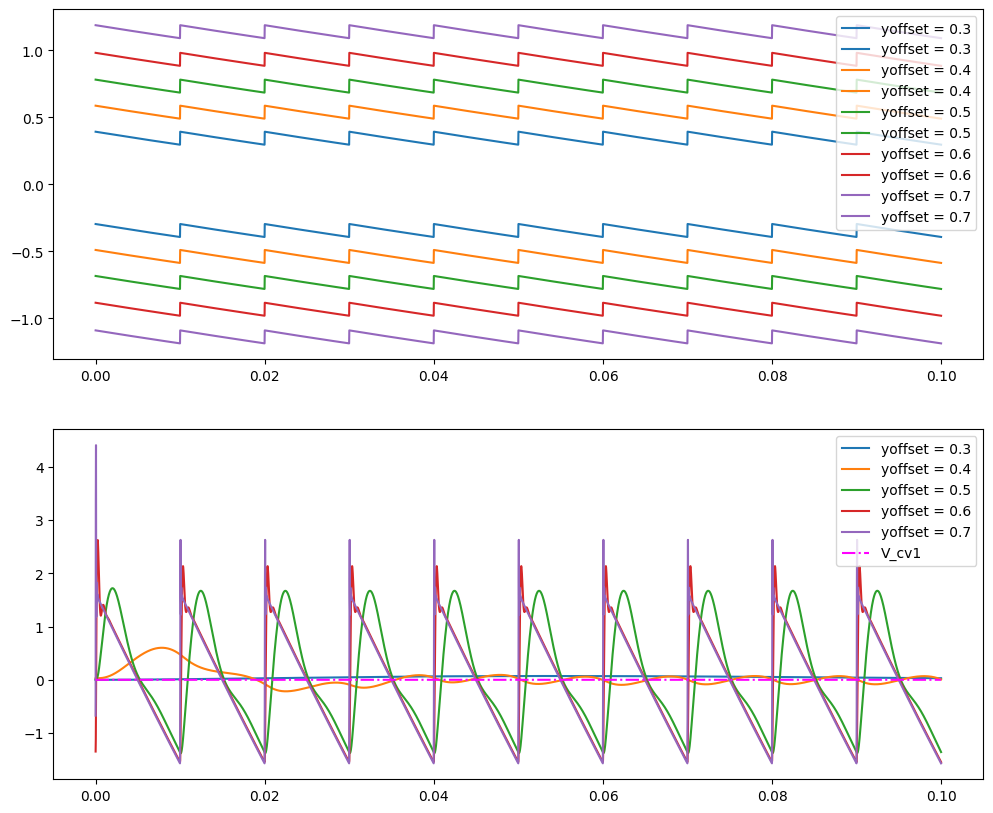

# the following is slow!

def generate_diode_ladder_full_resonance(
    ygain, tmax, ycv1=0.001, ycv2=0.001, wave=saw, yr=0.5, method="LUsolve"
):
    m = 1.0
    netlist = f"""
        # input and DC coupling
        V0 1 0 Vin
        Pgain 0 2 1 100000
        Cdc 2 3 1e-6
        R100k 3 4 100000
        R1k 4 0 1000
        Oamp 4 5 5       # buffer

        R33k 5 6 33000
        R33k 6 7 33000
        R2k 7 8 2000
        Oamp 0 6 8
        R33k 9 6 33000
        R33k 9 10 33000
        R33k 10 0 33000
        Oamp 10 11 12
        R33k 5 11 33000
        R33k 11 12 33000

        # 7 top of ladder, 12 bottom

        # cutoff and cv section
        Vneg1 13 0 -12.0
        R100k 13 9 100000
        R27k 9 0 27000
        Dcv 14 9
        Oamp 0 15 14
        R14k 14 15 14000
        Vpos 16 0 +12.0
        Vneg 18 0 -12.0
        Poffset 17 19 16 100000
        R27k 17 18 27000
        R100k 15 19 100000
        # cv inputs
        Vcv1 20 0 Vin_cv1
        Pcv1 0 21 20 100000
        R68k 21 15 68000
        Vcv2 22 0 Vin_cv2
        Pcv2 0 23 22 100000
        R68k 23 15 68000  

        # 7 top of ladder, 12 bottom
        D1 7 24
        C1 24 32 1e-9 m={m}
        D2 24 25
        C2 25 0 1e-9 m={m}
        D3 25 26
        C3 26 0 1e-9 m={m}
        D4 26 27
        C4 27 0 1e-9 m={m}
        D5 27 28
        C5 28 32 1e-9 m={m}
        D6 28 12    

        # resonance / output
        Oamp 26 29 29
        Pr 0 30 29 100000
        Oamp 30 31 32        
        R100k 31 32 100000
        Dp1 31 32
        Dp2 32 31 
        Rtrim 31 0 20000           # effectively trimmer

        # output gain stage and ac coupling
        R1k 29 33 1000
        Oamp 0 33 34
        R33k 33 34 33000
        Cac 34 35 1e-6
        R100k 35 0 100000
        Oamp 35 36 36

        J 36 0
        Jpos 7 0
        Jneg 12 0
    """

    R1k, R2k, R14k, R27k, R33k, R68k, R100k = symbols(
        "R1k, R2k, R14k, R27k, R33k, R68k, R100k"
    )
    Rpgain, Rpcv1, Rpcv2, Rpoffset, Rpr = symbols("Rpgain, Rpcv1, Rpcv2, Rpoffset, Rpr")
    assumptions = {
        R14k: 14 * R1k,
        R2k: 2 * R1k,
        R27k: 27 * R1k,
        R33k: 33 * R1k,
        R68k: 68 * R1k,
        R100k: 100 * R1k,
        Rpgain: 100 * R1k,
        Rpcv1: 100 * R1k,
        Rpcv2: 100 * R1k,
        Rpoffset: 100 * R1k,
        Rpr: 100 * R1k,
    }
    # assumptions = {}
    class_name = "DiodeLadderFull" + str(np.random.randint(100000))
    rules, (A, x, b) = run_MNA(
        netlist, class_name, method=method, simplify_sol=False, assumptions=assumptions
    )

    file_name = "diode_ladder_full"
    code_string = generate_processor(rules)

    for item in code_string.split("\n"):
        if "process" in item:
            print(class_name)
            print(item.strip())
    # print(code_string)

    dt = 1.0 / 44100.0
    ts = np.arange(0, tmax, dt)
    wave_fn = wave(freq=100, ppv=10)
    v_ins = wave_fn(ts)
    v_cv1, v_cv2 = 0.0, 0.0
    v_cv1s = np.linspace(0, 2, len(v_ins))

    with ModuleLoader(code_string, class_name) as m:
        fig, axs = plt.subplots(2, 1, figsize=(12, 10))

        for i, yoffset in enumerate([0.3, 0.4, 0.5, 0.6, 0.7]):
            m.reset()
            v_outs = []
            for v_in, v_cv1 in zip(v_ins, v_cv1s):
                outs = m.process(v_in, v_cv1, v_cv2, ycv1, ycv2, ygain, yoffset, yr, dt)
                v_outs.append(outs)
            v_outs = np.array(v_outs)

            axs[0].plot(ts, v_outs[:, 0], label=f"yoffset = {yoffset}")
            axs[1].plot(ts, v_outs[:, 1], label=f"yoffset = {yoffset}", color=colors[i])
            axs[1].plot(ts, v_outs[:, 2], label=f"yoffset = {yoffset}", color=colors[i])
            # axs[1].plot(ts, v_outs[:, 3], label=f'yoffset = {yoffset}', color=colors[i])

        axs[0].plot(ts, v_ins, "--", color="k", label=f"input")
        axs[0].plot(ts, v_cv1s, "-.", color="magenta", label=f"V_cv1")
        axs[0].legend()
        axs[1].legend()
        plt.show()

    return class_name, code_string, v_outs, rules


class_name_full, code_string_full, outs, rules = generate_diode_ladder_full_resonance(
    method="LUsolve", ygain=0.99, tmax=0.05, ycv1=0.2, yr=0.5
)
print(code_string_full)

DiodeLadderFull21319
auto process(float Vin, float Vin_cv1, float Vin_cv2, float ycv1, float ycv2, float ygain, float yoffset, float yr, float T) {

// generated with spice.hpp at 4375c34
class DiodeLadderFull21319 {
public:
    DiodeLadderFull21319()
        : cdc(1e-06, 0.5),
          dcv(0.0),
          d1(0.0),
          c1(1e-09, 1.0),
          d2(0.0),
          c2(1e-09, 1.0),
          d3(0.0),
          c3(1e-09, 1.0),
          d4(0.0),
          c4(1e-09, 1.0),
          d5(0.0),
          c5(1e-09, 1.0),
          d6(0.0),
          dp1(0.0),
          dp2(0.0),
          cac(1e-06, 0.5) {}

    // solution / device variables
    Capacitor cdc;
    Diode dcv;
    Diode d1;
    Capacitor c1;
    Diode d2;
    Capacitor c2;
    Diode d3;
    Capacitor c3;
    Diode d4;
    Capacitor c4;
    Diode d5;
    Capacitor c5;
    Diode d6;
    Diode dp1;
    Diode dp2;
    Capacitor cac;
    float v_2 = 0.f, v_2_prev = 0.f;
    float v_3 = 0.f, v_3_prev = 0.f;
    float v_7 = 0.f, v_7_prev = 0.f;
    float v_9 = 0.f, v_9_prev = 0.f;
    float v_12 = 0.f, v_12_prev = 0.f;
    float v_14 = 0.f, v_14_prev = 0.f;
    float v_24 = 0.f, v_24_prev = 0.f;
    float v_25 = 0.f, v_25_prev = 0.f;
    float v_26 = 0.f, v_26_prev = 0.f;
    float v_27 = 0.f, v_27_prev = 0.f;
    float v_28 = 0.f, v_28_prev = 0.f;
    float v_31 = 0.f, v_31_prev = 0.f;
    float v_32 = 0.f, v_32_prev = 0.f;
    float v_34 = 0.f, v_34_prev = 0.f;
    float v_35 = 0.f, v_35_prev = 0.f;
    float v_36 = 0.f, v_36_prev = 0.f;

    // dummy variable for storing stuff to expose to pybind
    float aux = 0.f;
    int iter = 0;
    auto process(float Vin, float Vin_cv1, float Vin_cv2, float ycv1, float ycv2, float ygain, float yoffset, float yr, float T) {
        // constants
        const float R1k = 1000;
        const float Vneg1 = -12.0;
        const float Vpos = 12.0;
        const float Vneg = -12.0;
        const float Rtrim = 20000;

        for (iter = 0; iter < MAX_ITER; ++iter) {
            // solution
            const float x0 = 1.0 / R1k;
            const float x1 = (1.0 / 100.0) * x0;
            const float x2 = ygain - 1;
            const float x3 = R1k * x2 * ygain;
            const float x4 = cdc.gc * x3;
            const float x5 = 1.0 / (x4 - 1.0 / 100.0);
            const float x6 = x3 * x5;
            const float x7 = 1.0 / (-pow(cdc.gc, 2) * x6 + cdc.gc + x1);
            const float x8 = pow(R1k, -2);
            const float x9 = x7 * x8;
            const float x10 = 11 * R1k;
            const float x11 = (1.0 / 99.0) * x0;
            const float x12 = d6.geq + x11;
            const float x13 = 1.0 / x12;
            const float x14 = (101.0 / 300.0) * x0 - 1.0 / 30000.0 * x9;
            const float x15 = x13 * x14;
            const float x16 = pow(d6.geq, 2);
            const float x17 = pow(d5.geq, 2);
            const float x18 = c4.gc + d4.geq + d5.geq;
            const float x19 = 1.0 / x18;
            const float x20 = 1.0 / (c5.gc + d5.geq + d6.geq - x13 * x16 - x17 * x19);
            const float x21 = pow(x12, -2);
            const float x22 = x16 * x20 * x21;
            const float x23 = x14 * x22;
            const float x24 = pow(c1.gc, 2);
            const float x25 = pow(d1.geq, 2);
            const float x26 = d1.geq + (35.0 / 66.0) * x0;
            const float x27 = 1.0 / x26;
            const float x28 = (1.0 / 2.0) * x0;
            const float x29 = 1.0 / (-1.0 / 4.0 * x27 * x8 + x28);
            const float x30 = x29 / pow(x26, 2);
            const float x31 = (1.0 / 4.0) * x30 * x8;
            const float x32 = c1.gc + d1.geq + d2.geq - x25 * x27 - x25 * x31;
            const float x33 = 1.0 / x32;
            const float x34 = dp1.geq + dp2.geq + x1;
            const float x35 = -x34;
            const float x36 = 1.0 / (x34 + 1.0 / Rtrim);
            const float x37 = c5.gc * x20;
            const float x38 = d4.geq * d5.geq * x19;
            const float x39 = c1.gc * x33;
            const float x40 = pow(d2.geq, 2);
            const float x41 = 1.0 / (c2.gc + d2.geq + d3.geq - x33 * x40);
            const float x42 = d3.geq * x41;
            const float x43 = d2.geq * x42;
            const float x44 = x37 * x38 + x39 * x43;
            const float x45 = -x44;
            const float x46 = yr - 101.0 / 100.0;
            const float x47 = 1.0 / x46;
            const float x48 = (1.0 / 100.0) * x47;
            const float x49 = x36 * (-x34 - x45 * x48);
            const float x50 = x40 * x41 / pow(x32, 2);
            const float x51 = c1.gc - pow(c5.gc, 2) * x20 + c5.gc - x24 * x33 - x24 * x50 + x34 - x35 * x49;
            const float x52 = 1.0 / x51;
            const float x53 = d6.geq * x15;
            const float x54 = x36 * x48;
            const float x55 = x20 * x38;
            const float x56 = x53 * x55;
            const float x57 = x35 * x54 * x56 + x37 * x53;
            const float x58 = x52 * x57;
            const float x59 = d6.geq * x13;
            const float x60 = x37 * x59;
            const float x61 = x58 * x60;
            const float x62 =
                1.0 / (-33.0 / 2.0 * R1k * ((101.0 / 100.0) * x0 - 1.0 / 10000.0 * x9) -
                       x10 * ((101.0 / 200.0) * x0 - 1.0 / 20000.0 * x9) - 1.0 / 3.0 * x15 - 1.0 / 3.0 * x23 - 1.0 / 3.0 * x61);
            const float x63 = -x15 - x23 - x61;
            const float x64 = dcv.geq + (3197.0 / 29700.0) * x0;
            const float x65 = 1.0 / x64;
            const float x66 = x65 * x8;
            const float x67 = (2.0 / 3267.0) * x66;
            const float x68 = x13 * ((4.0 / 99.0) * x0 - x67);
            const float x69 = pow(dcv.geq, 2);
            const float x70 = pow(x64, -2);
            const float x71 = (1.0 / 14.0) * x0;
            const float x72 = 1.0 / (dcv.geq - x65 * x69 + x71);
            const float x73 = -2.0 / 3267.0 * x13 * x69 * x70 * x72 * x8;
            const float x74 = -2.0 / 3267.0 * x59 * x69 * x70 * x72 * x8;
            const float x75 = d6.geq * x68 + x74;
            const float x76 = x20 * x59;
            const float x77 = x75 * x76;
            const float x78 = x55 * x75;
            const float x79 = x35 * x54 * x78 + x37 * x75;
            const float x80 = x52 * x79;
            const float x81 = x60 * x80;
            const float x82 = (1.0 / 1089.0) * x66;
            const float x83 = dcv.geq * x65;
            const float x84 = x0 * x83;
            const float x85 = x13 * x84;
            const float x86 = (1.0 / 3.0) * x83 + (2.0 / 297.0) * x85;
            const float x87 = -1.0 / 33.0 * dcv.geq * x0 * x65 * x72 * x86;
            const float x88 = -x10 * ((2.0 / 33.0) * x0 - x82) - 1.0 / 3.0 * x68 - 1.0 / 3.0 * x77 - 1.0 / 3.0 * x81 - x87;
            const float x89 = x62 * x63;
            const float x90 = d1.geq * x27;
            const float x91 = x28 * x29;
            const float x92 = x90 * x91;
            const float x93 = c1.gc * x50;
            const float x94 = x39 * x92 + x92 * x93;
            const float x95 = x52 * x57 * x62 * x88 * x94 - x80 * x94;
            const float x96 = (1.0 / 33.0) * x0;
            const float x97 = (1.0 / 132.0) * x30 / pow(R1k, 3);
            const float x98 = -d1.geq * x97 - x90 * x96;
            const float x99 = x33 * x98;
            const float x100 = x13 * (-x11 - x67);
            const float x101 = d6.geq * x100 + x74;
            const float x102 = x101 * x55 + x43 * x99;
            const float x103 = x101 * x37 + x102 * x35 * x54 + x39 * x98 + x93 * x98;
            const float x104 = x103 * x52;
            const float x105 = x101 * x76;
            const float x106 = x104 * x60;
            const float x107 =
                -x10 * (-1.0 / 66.0 * x0 - x82) - 1.0 / 3.0 * x100 - 1.0 / 3.0 * x105 - 1.0 / 3.0 * x106 - x87 + 1.0 / 2.0;
            const float x108 =
                1.0 / (-x104 * x94 + x107 * x52 * x57 * x62 * x94 + (1.0 / 66.0) * x27 * x29 * x8 - x50 * x92 * x98 - x92 * x99);
            const float x109 = -x100 - x105 - x106 - x107 * x89 - x73;
            const float x110 = x108 * x109;
            const float x111 = 1.0 / (-x110 * x95 - x68 - x73 - x77 - x81 - x88 * x89);
            const float x112 = x72 * x83 * x96;
            const float x113 = x108 * x112;
            const float x114 = (1.0 / 33.0) * dcv.geq * x0 * x65 * x72 - x113 * x95;
            const float x115 = dcv.geq * x66;
            const float x116 = x36 * x47;
            const float x117 = (1.0 / 69300.0) * x115 * x116 * x38 * x72 * x76;
            const float x118 = -1.0 / 693.0 * x115 * x60 * x72 - x117 * x35;
            const float x119 = x118 * x52;
            const float x120 = x119 * x60;
            const float x121 = (1.0 / 2079.0) * x115 * x22 * x72 - 1.0 / 3.0 * x120 + x71 * x72 * x86;
            const float x122 = x58 * x62;
            const float x123 = -x119 * x94 + x121 * x122 * x94;
            const float x124 = x111 * ((1.0 / 693.0) * dcv.geq * x13 * x65 * x72 * x8 +
                                       (1.0 / 693.0) * dcv.geq * x16 * x20 * x21 * x65 * x72 * x8 - x110 * x123 - x120 - x121 * x89);
            const float x125 = 1.0 / ((1.0 / 14.0) * x0 * x72 - x113 * x123 - x114 * x124);
            const float x126 = -x104 + x107 * x122;
            const float x127 = x108 * x126;
            const float x128 = -x127 * x95 + x52 * x57 * x62 * x88 - x80;
            const float x129 = -x119 + x121 * x52 * x57 * x62 - x123 * x127 - x124 * x128;
            const float x130 = yr - 1;
            const float x131 = 1.0 / x130;
            const float x132 = x1 * x131;
            const float x133 = x0 * x47;
            const float x134 = -1.0 / 10000.0 * x131 * x133 - x132 / yr;
            const float x135 = pow(x51, -2);
            const float x136 = x134 * x36;
            const float x137 = x35 * x52;
            const float x138 = x136 * x137;
            const float x139 = x135 * x35 * x57 * x60 * x62;
            const float x140 = (1.0 / 3.0) * x136 * x139 * x94 + x138 * x94;
            const float x141 = (1.0 / 3.0) * x138 * x60;
            const float x142 = x111 * (c5.gc * d6.geq * x13 * x134 * x20 * x35 * x36 * x52 - x110 * x140 - x141 * x89);
            const float x143 = -x113 * x140 - x114 * x142;
            const float x144 = x125 * x129;
            const float x145 = pow(d4.geq, 2);
            const float x146 = c3.gc - pow(d3.geq, 2) * x41 + d3.geq + d4.geq - x145 * x17 * x20 / pow(x18, 2) - x145 * x19;
            const float x147 = (1.0 / 100.0) * x146 * x35 * x36 * x47 - x44;
            const float x148 = x147 * x52;
            const float x149 = x148 * x60;
            const float x150 = (1.0 / 3.0) * d4.geq * d5.geq * d6.geq * x13 * x19 * x20 - 1.0 / 3.0 * x149;
            const float x151 = x122 * x150 * x94 - x148 * x94 + x33 * x43 * x92;
            const float x152 = x111 * (d4.geq * d5.geq * d6.geq * x13 * x19 * x20 - x110 * x151 - x149 - x150 * x89);
            const float x153 = -x113 * x151 - x114 * x152;
            const float x154 = -x127 * x151 - x128 * x152 - x144 * x153 - x148 + x150 * x52 * x57 * x62;
            const float x155 = x130 * x47;
            const float x156 = R1k * x155;
            const float x157 = R1k * x130 * x45 * x47 * x52 * x57 - x156 * x56;
            const float x158 = x157 * x62;
            const float x159 = R1k * x103 * x130 * x45 * x47 * x52 - x102 * x156 - x107 * x158;
            const float x160 = x108 * x159;
            const float x161 = R1k * x130 * x45 * x47 * x52 * x79 - x156 * x78 - x158 * x88 - x160 * x95;
            const float x162 = R1k * x118 * x130 * x45 * x47 * x52 +
                               (1.0 / 693.0) * d4.geq * d5.geq * d6.geq * dcv.geq * x0 * x13 * x130 * x19 * x20 * x47 * x65 * x72 -
                               x121 * x158 - x123 * x160 - x124 * x161;
            const float x163 = x125 * x162;
            const float x164 =
                1.0 / (R1k * x130 * x147 * x45 * x47 * x52 - x146 * x156 - x150 * x158 - x151 * x160 - x152 * x161 - x153 * x163);
            const float x165 = x164 * (-x138 * x156 * x45 - x140 * x160 - x141 * x158 - x142 * x161 - x143 * x163 - x48);
            const float x166 = 1.0 / ((1.0 / 3.0) * c5.gc * d6.geq * x13 * x134 * x135 * x20 * x35 * x36 * x57 * x62 - x127 * x140 -
                                      x128 * x142 + x134 * x35 * x36 * x52 - x143 * x144 - x154 * x165);
            const float x167 = dp1.ieq - dp2.ieq;
            const float x168 = -x167;
            const float x169 = -c1.ieq;
            const float x170 = -d1.ieq;
            const float x171 = d1.ieq * x90;
            const float x172 = d1.geq * d1.ieq * x31;
            const float x173 = -d2.ieq - x169 - x170 - x171 - x172;
            const float x174 = c4.ieq + d4.ieq - d5.ieq;
            const float x175 = x174 * x19;
            const float x176 = c5.ieq + d5.geq * x175 + d5.ieq + d6.ieq * x59 - d6.ieq;
            const float x177 = x168 * x49;
            const float x178 = d2.geq * x39;
            const float x179 = -d3.ieq;
            const float x180 = x173 * x33;
            const float x181 = c2.ieq + d2.geq * x180 + d2.ieq + x179;
            const float x182 = x181 * x41;
            const float x183 = -c5.ieq + x167 + x169 + x173 * x39 + x176 * x37 - x177 + x178 * x182;
            const float x184 = -Vin * x1 / x2 + cdc.ieq;
            const float x185 = -cdc.ieq + x184 * x4 * x5;
            const float x186 = x176 * x20;
            const float x187 = -1.0 / 100.0 * d4.geq * d5.geq * d6.geq * x13 * x14 * x168 * x19 * x20 * x36 * x47 + d6.ieq * x15 -
                               1.0 / 100.0 * x0 * x185 * x7 + x183 * x58 + x186 * x53;
            const float x188 = -x187 * x62;
            const float x189 = d1.ieq * x27;
            const float x190 = Vneg1 * x1;
            const float x191 = (2.0 / 99.0) * x85;
            const float x192 = d6.ieq * x191 + dcv.ieq * x83 - dcv.ieq + x190 * x83;
            const float x193 =
                -1.0 / 3300.0 * Vneg1 * x65 * x8 - 1.0 / 33.0 * dcv.geq * x0 * x192 * x65 * x72 - 1.0 / 33.0 * dcv.ieq * x0 * x65;
            const float x194 = d1.ieq * x97 + d2.geq * x182 * x99 + d6.ieq * x100 + x101 * x186 -
                               1.0 / 100.0 * x102 * x168 * x36 * x47 + x104 * x183 + x107 * x188 + x180 * x98 + x189 * x96 + x193;
            const float x195 = -x108 * x194;
            const float x196 = -1.0 / 100.0 * d4.geq * d5.geq * x168 * x19 * x20 * x36 * x47 * x75 + d6.ieq * x68 + x183 * x80 +
                               x186 * x75 + x188 * x88 + x193 + x195 * x95;
            const float x197 = -x196;
            const float x198 = (1.0 / 4.0) * x0;
            const float x199 = yoffset - 1;
            const float x200 = 1.0 / x199;
            const float x201 = x0 / (100 * yoffset + 27);
            const float x202 = 1.0 / yoffset;
            const float x203 = Vin_cv1 * x198 * ycv1 / (25 * ycv1 * (ycv1 - 1) - 17) +
                               Vin_cv2 * x198 * ycv2 / (25 * ycv2 * (ycv2 - 1) - 17) -
                               1.0 / 693.0 * d6.geq * dcv.geq * x13 * x176 * x20 * x65 * x72 * x8 - 1.0 / 14.0 * x0 * x192 * x72 -
                               1.0 / 100.0 * x0 * (Vneg * x201 - Vpos * x1 * x200) /
                                   ((1.0 / 100.0) * x0 * x200 * x202 * (x199 * yoffset - 1) - 27.0 / 100.0 * x201 * x202) +
                               x117 * x168 + x119 * x183 + x121 * x188 + x123 * x195 + x124 * x197;
            const float x204 = -x125 * x203;
            const float x205 = x148 * x183;
            const float x206 = x150 * x188;
            const float x207 = x151 * x195;
            const float x208 = x152 * x197;
            const float x209 = x153 * x204;
            const float x210 = c3.ieq + d3.ieq + d4.geq * x175 - d4.ieq + x146 * x168 * x54 + x181 * x42 + x186 * x38 - x205 - x206 -
                               x207 - x208 - x209;
            const float x211 =
                x134 * x183 * x35 * x36 * x52 - x136 * x168 - x140 * x195 - x141 * x188 - x142 * x197 - x143 * x204 - x165 * x210;
            const float x212 = x166 * x211;
            const float x213 = c3.ieq + d3.geq * x181 * x41 + d4.geq * d5.geq * x176 * x19 * x20 + d4.geq * x174 * x19 - d4.ieq +
                               (1.0 / 100.0) * x146 * x168 * x36 * x47 - x154 * x212 - x179 - x205 - x206 - x207 - x208 - x209;
            const float x214 = x164 * x213;
            const float x215 = x125 * (-x129 * x212 - x162 * x214 - x203);
            const float x216 = x111 * (-x114 * x215 - x128 * x212 - x161 * x214 - x196);
            const float x217 = -x109 * x216 - x112 * x215 - x126 * x212 - x159 * x214 - x194;
            const float x218 = x62 * (x108 * x217 * x52 * x57 * x94 - x157 * x214 + x166 * x211 * x52 * x57 - x187 - x216 * x63);
            const float x219 = (1.0 / 3.0) * x218;
            const float x220 = -x219;
            const float x221 = x216 * x59;
            const float x222 = x221 * x37;
            const float x223 = x108 * x217;
            const float x224 = x223 * x94;
            const float x225 = x219 * x59;
            const float x226 =
                x52 * (R1k * x130 * x164 * x213 * x45 * x47 + c1.gc * d2.geq * x181 * x33 * x41 + c1.gc * x173 * x33 - c1.ieq +
                       c5.gc * x176 * x20 - c5.ieq + dp1.ieq - dp2.ieq - x177 - x212 - x222 - x224 - x225 * x37);
            const float x227 = x36 * (-x167 - x226 * x35);
            const float x228 = x156 * (-x132 * x227 - x214);
            const float x229 = x20 * (c5.gc * x226 + x176 - x221 - x225 + x228 * x38);
            const float x230 = x13 * (d6.geq * x229 + d6.ieq - x216 + x220);
            const float x231 = x0 * x230;
            const float x232 = x7 * (x185 - 11.0 / 50.0 * x218 + (1.0 / 300.0) * x231);
            const float x233 = x223 * x92;
            const float x234 = x41 * (-d2.geq * x233 * x33 + d3.geq * x228 + x178 * x226 + x181);
            const float x235 = c1.gc * x226 + c1.ieq + d1.ieq + d2.geq * x234 - d2.ieq - x171 - x172 - x233;
            const float x236 = x235 * x33;
            const float x237 = x72 * (-x191 * x216 + x192 - x215 - x218 * x86 + (2.0 / 99.0) * x229 * x59 * x84);
            const float x238 = cac.gc + x96;
            const float x239 = 1.0 / x238;
            const float x240 = 1.0 / cac.gc;
            const float x241 = -pow(cac.gc, 2) * x239 + cac.gc + x1;
            const float x242 = x240 * x241;
            const float x243 = x239 * x96;
            const float x244 = x1 * x116;
            const float x245 = x168 * x244;
            const float x246 = x137 * x244;
            const float x247 = x116 * x238 * x242;
            const float x248 = x137 * x247;
            const float x249 = (11.0 / 100.0) * x248 * x60;
            const float x250 = (11.0 / 100.0) * x139 * x247 * x94 + (33.0 / 100.0) * x248 * x94;
            const float x251 = x111 * ((33.0 / 100.0) * c5.gc * d6.geq * x13 * x20 * x238 * x240 * x241 * x35 * x36 * x47 * x52 -
                                       x110 * x250 - x249 * x89);
            const float x252 = -x113 * x250 - x114 * x251;
            const float x253 = x137 * x36;
            const float x254 = -1.0 / 100.0 * x130 * x253 * x45 / pow(x46, 2) + x155;
            const float x255 = x164 * (33 * R1k * x238 * x240 * x241 * x254 - x158 * x249 - x160 * x250 - x161 * x251 - x163 * x252);
            const float x256 =
                (33 * R1k * x238 * x240 * x241 * (cac.ieq * x243 + x183 * x246 - x245) + cac.gc * cac.ieq * x239 - cac.ieq -
                 x188 * x249 - x195 * x250 - x197 * x251 - x204 * x252 - x210 * x255 -
                 x212 * ((11.0 / 100.0) * c5.gc * d6.geq * x13 * x135 * x20 * x238 * x240 * x241 * x35 * x36 * x47 * x57 * x62 -
                         x127 * x250 - x128 * x251 - x144 * x252 - x154 * x255 +
                         (33.0 / 100.0) * x238 * x240 * x241 * x35 * x36 * x47 * x52)) /
                (cac.gc * x239 + x242);
            const float x257 =
                33 * R1k * x238 *
                ((1.0 / 33.0) * cac.ieq * x0 * x239 + (1.0 / 100.0) * x0 * x183 * x35 * x36 * x47 * x52 -
                 1.0 / 300.0 * x133 * x218 * x253 * x60 - x212 * x246 - x214 * x254 - x222 * x246 - x224 * x246 - x243 * x256 - x245);
            const float x258 = -x240 * x257;
            v_2 = x6 * (cdc.gc * x232 + x184);
            v_3 = x232;
            v_7 = x27 * (d1.geq * x236 + x170 + x91 * ((1.0 / 2.0) * d1.geq * x0 * x235 * x27 * x33 - x189 * x28 - x223));
            v_9 = x65 * (dcv.geq * x237 + dcv.ieq + x190 + x220 + (2.0 / 99.0) * x231);
            v_12 = x230;
            v_14 = x237;
            v_24 = x236;
            v_25 = x234;
            v_26 = x228;
            v_27 = x19 * (d4.geq * x228 + d5.geq * x229 + x174);
            v_28 = x229;
            v_31 = x227;
            v_32 = x226;
            v_34 = x239 * (cac.ieq - x256 - x257);
            v_35 = x258;
            v_36 = x258;

            // linearisation / newton
            dcv.newton(v_14 - v_9);
            d1.newton(-v_24 + v_7);
            d2.newton(v_24 - v_25);
            d3.newton(v_25 - v_26);
            d4.newton(v_26 - v_27);
            d5.newton(v_27 - v_28);
            d6.newton(-v_12 + v_28);
            dp1.newton(v_31 - v_32);
            dp2.newton(-v_31 + v_32);

            // convergence check
            bool converged = true;
            converged = converged & (std::abs(v_2 - v_2_prev) < EPS);
            converged = converged & (std::abs(v_3 - v_3_prev) < EPS);
            converged = converged & (std::abs(v_7 - v_7_prev) < EPS);
            converged = converged & (std::abs(v_9 - v_9_prev) < EPS);
            converged = converged & (std::abs(v_12 - v_12_prev) < EPS);
            converged = converged & (std::abs(v_14 - v_14_prev) < EPS);
            converged = converged & (std::abs(v_24 - v_24_prev) < EPS);
            converged = converged & (std::abs(v_25 - v_25_prev) < EPS);
            converged = converged & (std::abs(v_26 - v_26_prev) < EPS);
            converged = converged & (std::abs(v_27 - v_27_prev) < EPS);
            converged = converged & (std::abs(v_28 - v_28_prev) < EPS);
            converged = converged & (std::abs(v_31 - v_31_prev) < EPS);
            converged = converged & (std::abs(v_32 - v_32_prev) < EPS);
            converged = converged & (std::abs(v_34 - v_34_prev) < EPS);
            converged = converged & (std::abs(v_35 - v_35_prev) < EPS);
            converged = converged & (std::abs(v_36 - v_36_prev) < EPS);
            if (converged) {
                break;
            }
            v_2_prev = v_2;
            v_3_prev = v_3;
            v_7_prev = v_7;
            v_9_prev = v_9;
            v_12_prev = v_12;
            v_14_prev = v_14;
            v_24_prev = v_24;
            v_25_prev = v_25;
            v_26_prev = v_26;
            v_27_prev = v_27;
            v_28_prev = v_28;
            v_31_prev = v_31;
            v_32_prev = v_32;
            v_34_prev = v_34;
            v_35_prev = v_35;
            v_36_prev = v_36;
        }

        // state updates (caps etc)
        cdc.tick(-v_2 + v_3, T);
        c1.tick(-v_24 + v_32, T);
        c2.tick(-v_25, T);
        c3.tick(-v_26, T);
        c4.tick(-v_27, T);
        c5.tick(-v_28 + v_32, T);
        cac.tick(-v_34 + v_35, T);

        // outputs
        const float jout = v_36;
        const float jout_pos = v_7;
        const float jout_neg = v_12;
        return std::make_tuple(jout, jout_pos, jout_neg);
    }

    void reset() {
        cdc.reset();
        c1.reset();
        c2.reset();
        c3.reset();
        c4.reset();
        c5.reset();
        cac.reset();
        v_2 = v_2_prev = 0.f;
        v_3 = v_3_prev = 0.f;
        v_7 = v_7_prev = 0.f;
        v_9 = v_9_prev = 0.f;
        v_12 = v_12_prev = 0.f;
        v_14 = v_14_prev = 0.f;
        v_24 = v_24_prev = 0.f;
        v_25 = v_25_prev = 0.f;
        v_26 = v_26_prev = 0.f;
        v_27 = v_27_prev = 0.f;
        v_28 = v_28_prev = 0.f;
        v_31 = v_31_prev = 0.f;
        v_32 = v_32_prev = 0.f;
        v_34 = v_34_prev = 0.f;
        v_35 = v_35_prev = 0.f;
        v_36 = v_36_prev = 0.f;
    }

    void calculateDC(float Vin, float Vin_cv1, float Vin_cv2, float ycv1, float ycv2, float ygain, float yoffset, float yr, float T) {}
};