spiceworld - Introduction and Preliminaries

There are far better resources than here to explain in detail the principles behind simulating circuits with MNA. Some good places to start would be:

However the basic principles can be illustrated with a few examples. Let’s look at the circuit below from the Swarthmore College site (note with node names a->1, b->2, c->3):

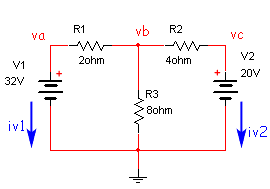
Circuits such as this can be described by a netlist, a list of commands of the form <identifier> <node_1> ... <node_n> <value> <other_params>. So for a 4 ohm resistor between nodes 2 and 3: R2 2 3 4.0.

netlist = """
V1 1 0 32.
R1 1 2 2
R2 2 3 4
R3 2 0 8
V2 3 0 20    
"""

In order to solve for the unknown node voltages, we can apply Kirchoff’s current law, plus equations for each voltage source:

_, (A, x, b) = run_MNA(netlist, "Example")

for i, (lhs, rhs) in enumerate(zip(A * x, b), start=1):
    display(Eq(lhs, rhs))

$i_{v 1} + \frac{v_{1}}{R_{1}} - \frac{v_{2}}{R_{1}} = 0$

$v_{2} \cdot (\frac{1}{R_{3}} + \frac{1}{R_{2}} + \frac{1}{R_{1}}) - \frac{v_{3}}{R_{2}} - \frac{v_{1}}{R_{1}} = 0$

$i_{v 2} - \frac{v_{2}}{R_{2}} + \frac{v_{3}}{R_{2}} = 0$

$v_{1} = V_{1}$

$v_{3} = V_{2}$

This can be formulated as a matrix problem $A x = b$ where $A$ is a matrix describing the (inverse) resistances between nodes, $x$ is a vector of unknown voltages and currents, and $b$ is a vector of known sources.

display(Eq(MatMul(A, x), b))

$[\begin{matrix} \frac{1}{R_{1}} & - \frac{1}{R_{1}} & 0 & 1 & 0 \\ - \frac{1}{R_{1}} & \frac{1}{R_{3}} + \frac{1}{R_{2}} + \frac{1}{R_{1}} & - \frac{1}{R_{2}} & 0 & 0 \\ 0 & - \frac{1}{R_{2}} & \frac{1}{R_{2}} & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{matrix}] [\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \\ i_{v 1} \\ i_{v 2} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ 0 \\ V_{1} \\ V_{2} \end{matrix}]$

In this form, we can easily solve for the unknown voltages and currents, e.g. by using LU decomposition:

display(Eq(x, simplify(A.LUsolve(b))))

$[\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \\ i_{v 1} \\ i_{v 2} \end{matrix}] = [\begin{matrix} V_{1} \\ \frac{R_{3} (R_{1} V_{2} + R_{2} V_{1})}{R_{1} R_{2} + R_{1} R_{3} + R_{2} R_{3}} \\ V_{2} \\ \frac{- R_{2} V_{1} - R_{3} V_{1} + R_{3} V_{2}}{R_{1} R_{2} + R_{1} R_{3} + R_{2} R_{3}} \\ \frac{- R_{1} V_{2} + R_{3} V_{1} - R_{3} V_{2}}{R_{1} R_{2} + R_{1} R_{3} + R_{2} R_{3}} \end{matrix}]$

This is one of the most basic examples we could consider. Things get much more interesting when we introduce time dependent components such as capacitors and nonlinear elements such as diodes. We’ll consider these in future posts.